THE UNIVERSITY OF BRITISH COLUMBIA
Physics 438
Assignment #
1:
METABOLISM
SOLUTIONS:
Tue. 09 Jan. 2007 - finish by Tue. 23 Jan.
The first part of this assignment was not for credit,
but most people did it anyway! We appreciate those who
Updated their Profiles, especially if they
gave us their preferred Email address in the database.
(To those who weren't able to get around to it in the first two weeks:
it's never too late! The database awaits your input/revisions
for the duration of the course.)
- GET CONNECTED:
Go to the 438 Homepage at
http://musr.physics.ubc.ca/p438/ and
- Browse.
Make sure you know what's there, how to get to it
and what it's good for (if anything).
Email jess@physics.ubc.ca if you have any questions.
- Make sure you can log in on that site
and that there is one and only one entry for you
in the 438 People Database.
Your User ID and your initial password
are both set to your student number.
You may wish to change your password.1
Your Profile in the 438 People Database has fields for
all sorts of information about you, most of which are blank.
You may want to Update your Profile, either to add/correct
said information or to alter your privacy setting
(at the bottom of the Update form).
- Repeat the steps above for the 438 WebCT site2
(to which there is a link on the 438 Homepage).
This site is handy for certain things like Discussions,
tentative Marks and your own personal 438 Homepage
(if you'd like one); we may also use it for other things like
chat or whiteboard work; if you have an idea for
more creative uses of WebCT, please tell us about it.
- Send us an Email containing a brief
description of who you are, what talents and skills you bring to
the 438 community, and what you hope to get out of the course.
Please send this to jess@physics.ubc.ca and
jergold@zoology.ubc.ca and aweber@physics.ubc.ca
from your own preferred Email address, so we will all know
how to contact each other in emergencies.
For the rest of the Assignment (and for all subsequent Assignments),
join a group of 3-5 students.
Please hand in one assignment per group
and list the names & Email addresses of all group members
at the top of each sheet.
In general, if you think some necessary information is missing,
make a reasonable assumption. But always write down
what that assumption is.
- STAIRCASE OLYMPICS:
- Determine the mechanical power output3
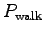 for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
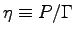 , we have
, we have
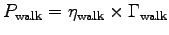 where
where
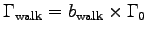 is the metabolic rate while walking up the stairs
and
is the metabolic rate while walking up the stairs
and 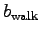 is the corresponding metabolic activity factor.
Calculate
is the corresponding metabolic activity factor.
Calculate
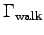 and
and 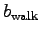 for each team member.
What value should you take for
for each team member.
What value should you take for 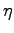 ? Discuss this choice
and comment upon its validity in your written report.
ANSWER:
Work is defined as the product of a force F times the distance x
over which the force needs to be overcome.
In our case the force to overcome is the gravitational force
Fg = M x g over the height h.
Now, the power P is the amount of energy used per time.
In our case:
? Discuss this choice
and comment upon its validity in your written report.
ANSWER:
Work is defined as the product of a force F times the distance x
over which the force needs to be overcome.
In our case the force to overcome is the gravitational force
Fg = M x g over the height h.
Now, the power P is the amount of energy used per time.
In our case:
This power needs to come from somewhere,
which in the end is provided by the power produced by our metabolism.
Since the metabolism needs also to produce power
to keep your body functions working (e.g. heat),
the total metabolic power produced during the climb
is only partly used for the actual climb.
Therefore
where 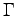 is the metabolic rate and
is the metabolic rate and 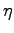 the efficiency,
which we don't know(!) but we have to assume some value,
so we assume the "typical" value given in the textbook,
namely 25%.
Then the metabolic activity factor
the efficiency,
which we don't know(!) but we have to assume some value,
so we assume the "typical" value given in the textbook,
namely 25%.
Then the metabolic activity factor
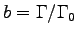 can be determined from
can be determined from 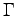 by assuming that
by assuming that 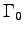 is given by the "mouse to elephant" allometric relation.
is given by the "mouse to elephant" allometric relation.
For example, to calculate the metabolic activity factor b
when M = 60 kg, h = 7.3 m and t = 20 s, we first find
and then estimate the resting metabolic rate
Now,
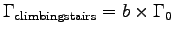 ,
so the activity factor is
,
so the activity factor is
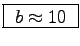 .
.
- Estimate your uncertainty in this measurement.5 The largest possible value,
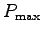 , is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time
, is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time 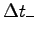 .
Similarly combine the lowest likely body mass M-
and the longest likely time
.
Similarly combine the lowest likely body mass M-
and the longest likely time 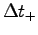 to find a value for
to find a value for 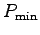 .
A good estimate of the uncertainty in your experimental result
is thus
.
A good estimate of the uncertainty in your experimental result
is thus
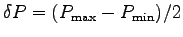 .
Express your answer for the power
.
Express your answer for the power 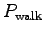 in the form
in the form
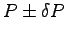 W. (Always include units.)
ANSWER:
You have an uncertainty in your body mass
(clothes, amount of water you have drunk, . . . )
which we assume for this example to be
W. (Always include units.)
ANSWER:
You have an uncertainty in your body mass
(clothes, amount of water you have drunk, . . . )
which we assume for this example to be
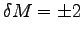 kg
and an uncertainty in time
kg
and an uncertainty in time
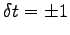 s.
We want to calculate the uncertainty in our calculation results.
Using the prescription above with the example numbers,
we get
s.
We want to calculate the uncertainty in our calculation results.
Using the prescription above with the example numbers,
we get
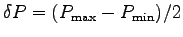 = (233.7 - 197.8)/2
= (233.7 - 197.8)/2
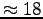 W so that
W so that
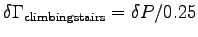 , giving
, giving
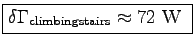 .7
.7
- Determine
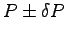 for each one of your team members
when running up the stairs.8 ANSWER:
If the same person runs up the stairs in t = 10 s we get
for each one of your team members
when running up the stairs.8 ANSWER:
If the same person runs up the stairs in t = 10 s we get
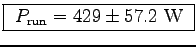 and
and
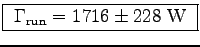 ,
assuming the same uncertainties as before.
,
assuming the same uncertainties as before.
- Estimate the mass of the muscles
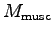 used for running up the stairs and give the power to mass ratio
used for running up the stairs and give the power to mass ratio
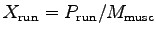 of these muscles.9 Muscle mass (
of these muscles.9 Muscle mass (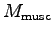 ) = muscle volume (
) = muscle volume (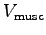 )
times muscle density (
)
times muscle density (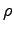 ).
Muscles have about the same density as water.
ANSWER:
The mean leg muscle mass of 60 kg women is measured to be 15 kg
using X-ray absortiometry.10 Thus the power-to-weight ratio for the running muscles
(assuming the leg muscles do almost all the work) is
).
Muscles have about the same density as water.
ANSWER:
The mean leg muscle mass of 60 kg women is measured to be 15 kg
using X-ray absortiometry.10 Thus the power-to-weight ratio for the running muscles
(assuming the leg muscles do almost all the work) is
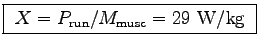 .
.
- Make a table including all your data showing
Name, M,
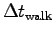 ,
, 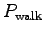 ,
,
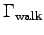 ,
,
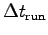 ,
, 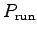 ,
,
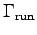 ,
,
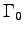 ,
, 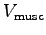 and
and 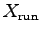 ,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
ANSWER:
The tables will be different for each group.
Uncertainties fall into two categories:
measurement imprecision and theoretical imprecision.
In the former category are your elapsed time
(probably measured to about
,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
ANSWER:
The tables will be different for each group.
Uncertainties fall into two categories:
measurement imprecision and theoretical imprecision.
In the former category are your elapsed time
(probably measured to about 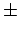 1 s) and
your mass (probably estimated to about
1 s) and
your mass (probably estimated to about 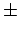 1-2 kg,
including clothes etc.).
In the latter category is your efficiency
1-2 kg,
including clothes etc.).
In the latter category is your efficiency 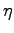 ,
which you had to guess in order to convert
P into
,
which you had to guess in order to convert
P into 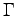 , and your resting metabolism
, and your resting metabolism 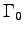 ,
which you had to assume could be estimated from
the "mouse-to-elephant" allometric relation,
,
which you had to assume could be estimated from
the "mouse-to-elephant" allometric relation,
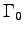 [W] = 4 M[kg]0.75 - which we know is
not a precise law but merely a consistent trend,
with typical deviations of about a factor of two!
A similar "slop" can be expected for the efficiency,
which is only "typically" 25%.
So you should not be expect these calculations to yield
"true" values of your activity factor, were you to
measure same more directly using oxygen consumption etc.
As with all estimations of uncertainty, a good deal of
subjective judgement is necessary;
just be sure you can explain why
you give the estimate you do.
[W] = 4 M[kg]0.75 - which we know is
not a precise law but merely a consistent trend,
with typical deviations of about a factor of two!
A similar "slop" can be expected for the efficiency,
which is only "typically" 25%.
So you should not be expect these calculations to yield
"true" values of your activity factor, were you to
measure same more directly using oxygen consumption etc.
As with all estimations of uncertainty, a good deal of
subjective judgement is necessary;
just be sure you can explain why
you give the estimate you do.
Compound table for those who submitted data:
| Weight |
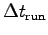 [s] [s] |
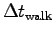 [s] [s] |
| 51.8 kg |
30 |
64 |
| 74.8 kg |
18 |
60 |
| 79 kg |
18 |
|
| 57 kg |
|
103 |
| 59 kg |
32 |
65 |
| 140 lb |
25 |
|
| 135 lb |
25 |
64 |
| 90 kg |
69 |
110 |
| 135 lb |
30 |
68 |
| 56 kg |
24 |
106 |
| 120 lb |
17 |
61 |
- Make a log-log graph for each of
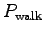 ,
, 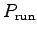 ,
,
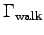 ,
,
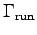 ,
,
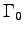 and
and 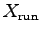 as functions of body mass M.
ANSWER:
This part will also be different for each group.
as functions of body mass M.
ANSWER:
This part will also be different for each group.
- SO SWEET SO MEAN:
A hummingbird weighing M = 3.9 g visits 1000 flowers daily
and thereby collects nectar with an energy content of
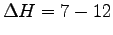 kcal [see R. Conniff 2000]11
kcal [see R. Conniff 2000]11
- Take an average value of
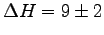 kcal.
What is the [sugar and]12 honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
ANSWER:
Let's treat nectar as a solution of honey in water.
The specific heat of combustion of glucose is hg= 4.15 kcal/g,
so the specific heat of combustion of honey is
kcal.
What is the [sugar and]12 honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
ANSWER:
Let's treat nectar as a solution of honey in water.
The specific heat of combustion of glucose is hg= 4.15 kcal/g,
so the specific heat of combustion of honey is
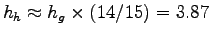 kcal/g.
kcal/g.
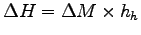 so
so
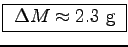 .
.
- Determine the metabolic rate
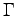 of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
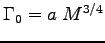 is applicable,
determine the constant a in that rate function.
ANSWER:
Basal metabolic rate scales as
is applicable,
determine the constant a in that rate function.
ANSWER:
Basal metabolic rate scales as
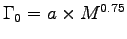 ;
the average daily metabolic rate for the hummingbird
can be expressed as
;
the average daily metabolic rate for the hummingbird
can be expressed as
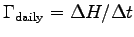 and therefore
and therefore
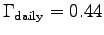 W.
using 4185 J/kcal with
W.
using 4185 J/kcal with
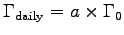 and
and
 kg, we find
kg, we find 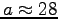 .
Therefore
.
Therefore
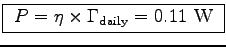 ,
using again
,
using again
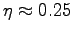 .
.
- Compare your calculated value of a with
the constant
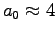 of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
ANSWER:
of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
ANSWER:
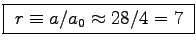 .
.
It is reasonable to assume that metabolic activity factors
vary among species and also vary among different activities.
However,
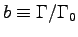 refers to the
refers to the 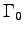 for that animal, so r is not b.
for that animal, so r is not b.
- What problems can you foresee for such a high metabolic rate?
ANSWER:
The high metabolic rate of hummingbirds is attributed to
their characteristic hovering flight and small body size.
This is probably accompanied by a very large daily energetic demand.
Hummingbirds also posses the greatest mass specific power for muscle:
98 W/kg.13
- Calculate the specific metabolic rate
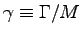 for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
ANSWER:
The specific metabolic rate for the hummingbird is
for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
ANSWER:
The specific metabolic rate for the hummingbird is
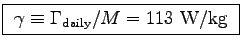 .
For an elephant, assuming M = 5000 kg and
.
For an elephant, assuming M = 5000 kg and
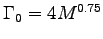 ,
,
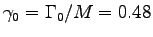 W/kg at rest,
which even with an activity factor of b = 10
would not get higher then roughly
W/kg at rest,
which even with an activity factor of b = 10
would not get higher then roughly
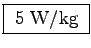 .
Pound for pound, the elephant utilizes energy far more efficiently.
.
Pound for pound, the elephant utilizes energy far more efficiently.
- HOT DEFENCES:
Giant hornets like to eat bee larvae and honey.
They are so strong that they can just invade a beehive
and kill the guards at the entrance
and get at their favourite food.
A certain strain of Japanese honey bees
has found a thermodynamic defence.
They can tolerate a temperature of
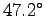 C (
C (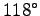 F).
The hornets however can only stand
F).
The hornets however can only stand 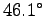 C (
C (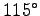 F).
The bees have learned to raise their body temperature
to
F).
The bees have learned to raise their body temperature
to 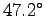 (
(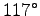 F):
they humm while contracting and relaxing their flight muscles,
and only generate heat without producing external mechanical work
. . . and thereby steam the hornets in their own juice.
Take a specific muscle power of p = P/M = 150 W/kg.
The specific heat of tissue is close to that of water.
Assume that the bees normally have a body temperature of
F):
they humm while contracting and relaxing their flight muscles,
and only generate heat without producing external mechanical work
. . . and thereby steam the hornets in their own juice.
Take a specific muscle power of p = P/M = 150 W/kg.
The specific heat of tissue is close to that of water.
Assume that the bees normally have a body temperature of 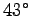 C
and that 10% of the body weight of a bee is muscle.
C
and that 10% of the body weight of a bee is muscle.
- How much heat energy must be generated by each bee
to reach the killing temperature?
ANSWER:
Heat energy:
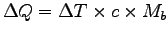 .
The specific heat of tissue is about that of water:
.
The specific heat of tissue is about that of water:
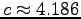 kJ kg-1 K-1.
Thus with
kJ kg-1 K-1.
Thus with
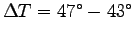 C
C 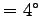 C
and
C
and
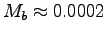 kg, we have
kg, we have
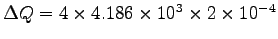 or
or
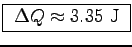 .
.
- What is the heating power of each bee?
ANSWER:
The mechanical power is the efficiency times the heating power:
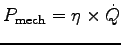 .
The specific muscle power
.
The specific muscle power
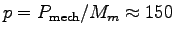 W/kg,
and so if
W/kg,
and so if
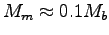 , with Mb = 0.0002 kg we get
the bee's muscle weight
, with Mb = 0.0002 kg we get
the bee's muscle weight
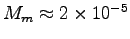 kg,
giving a muscle power
kg,
giving a muscle power
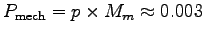 W.
Thus
W.
Thus
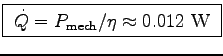 .
.
- How quickly do the bees reach the killing temperature?
ANSWER:
The flow of energy is identified with metabolic rate,
in this case a heating metabolic rate:
 with
with
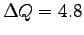 J.
Again,
J.
Again,
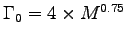 and since
and since
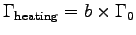 , b = 15
gives
, b = 15
gives
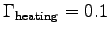 W. Thus
W. Thus
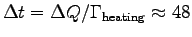 s
or
s
or
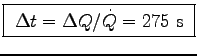 .
.
Alternatively:
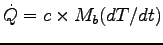 ; in this case,
0.012 W = 4.186 J/kg x 0.0002 kg
x (dT/dt)
giving
; in this case,
0.012 W = 4.186 J/kg x 0.0002 kg
x (dT/dt)
giving
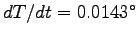 C/s. Thus
C/s. Thus
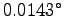 C/s
C/s
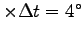 C
implies
C
implies
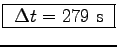 .
.
Jess H. Brewer
2007-02-17
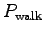 for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
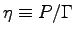 , we have
, we have
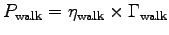 where
where
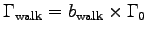 is the metabolic rate while walking up the stairs
and
is the metabolic rate while walking up the stairs
and 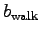 is the corresponding metabolic activity factor.
Calculate
is the corresponding metabolic activity factor.
Calculate
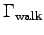 and
and 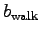 for each team member.
What value should you take for
for each team member.
What value should you take for 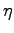 ? Discuss this choice
and comment upon its validity in your written report.
ANSWER:
Work is defined as the product of a force F times the distance x
over which the force needs to be overcome.
In our case the force to overcome is the gravitational force
Fg = M x g over the height h.
Now, the power P is the amount of energy used per time.
In our case:
? Discuss this choice
and comment upon its validity in your written report.
ANSWER:
Work is defined as the product of a force F times the distance x
over which the force needs to be overcome.
In our case the force to overcome is the gravitational force
Fg = M x g over the height h.
Now, the power P is the amount of energy used per time.
In our case:
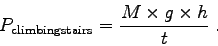
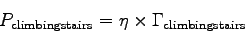
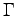 is the metabolic rate and
is the metabolic rate and 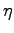 the efficiency,
which we don't know(!) but we have to assume some value,
so we assume the "typical" value given in the textbook,
namely 25%.
Then the metabolic activity factor
the efficiency,
which we don't know(!) but we have to assume some value,
so we assume the "typical" value given in the textbook,
namely 25%.
Then the metabolic activity factor
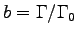 can be determined from
can be determined from 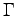 by assuming that
by assuming that 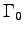 is given by the "mouse to elephant" allometric relation.
is given by the "mouse to elephant" allometric relation.
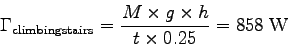
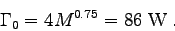
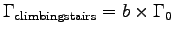 ,
so the activity factor is
,
so the activity factor is
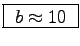 .
.
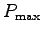 , is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time
, is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time 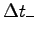 .
Similarly combine the lowest likely body mass M-
and the longest likely time
.
Similarly combine the lowest likely body mass M-
and the longest likely time 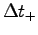 to find a value for
to find a value for 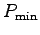 .
A good estimate of the uncertainty in your experimental result
is thus
.
A good estimate of the uncertainty in your experimental result
is thus
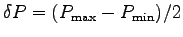 .
Express your answer for the power
.
Express your answer for the power 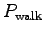 in the form
in the form
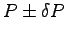 W. (Always include units.)
ANSWER:
You have an uncertainty in your body mass
(clothes, amount of water you have drunk, . . . )
which we assume for this example to be
W. (Always include units.)
ANSWER:
You have an uncertainty in your body mass
(clothes, amount of water you have drunk, . . . )
which we assume for this example to be
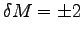 kg
and an uncertainty in time
kg
and an uncertainty in time
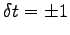 s.
We want to calculate the uncertainty in our calculation results.
Using the prescription above with the example numbers,
we get
s.
We want to calculate the uncertainty in our calculation results.
Using the prescription above with the example numbers,
we get
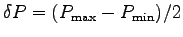 = (233.7 - 197.8)/2
= (233.7 - 197.8)/2
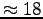 W so that
W so that
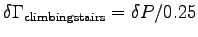 , giving
, giving
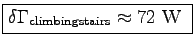 .7
.7
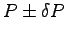 for each one of your team members
when running up the stairs.8 ANSWER:
If the same person runs up the stairs in t = 10 s we get
for each one of your team members
when running up the stairs.8 ANSWER:
If the same person runs up the stairs in t = 10 s we get
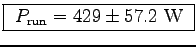 and
and
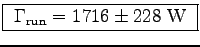 ,
assuming the same uncertainties as before.
,
assuming the same uncertainties as before.
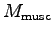 used for running up the stairs and give the power to mass ratio
used for running up the stairs and give the power to mass ratio
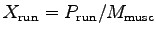 of these muscles.9 Muscle mass (
of these muscles.9 Muscle mass (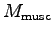 ) = muscle volume (
) = muscle volume (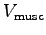 )
times muscle density (
)
times muscle density (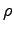 ).
Muscles have about the same density as water.
ANSWER:
The mean leg muscle mass of 60 kg women is measured to be 15 kg
using X-ray absortiometry.10 Thus the power-to-weight ratio for the running muscles
(assuming the leg muscles do almost all the work) is
).
Muscles have about the same density as water.
ANSWER:
The mean leg muscle mass of 60 kg women is measured to be 15 kg
using X-ray absortiometry.10 Thus the power-to-weight ratio for the running muscles
(assuming the leg muscles do almost all the work) is
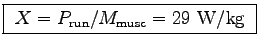 .
.
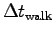 ,
, 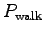 ,
,
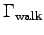 ,
,
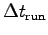 ,
, 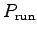 ,
,
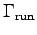 ,
,
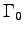 ,
, 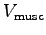 and
and 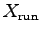 ,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
ANSWER:
The tables will be different for each group.
Uncertainties fall into two categories:
measurement imprecision and theoretical imprecision.
In the former category are your elapsed time
(probably measured to about
,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
ANSWER:
The tables will be different for each group.
Uncertainties fall into two categories:
measurement imprecision and theoretical imprecision.
In the former category are your elapsed time
(probably measured to about 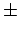 1 s) and
your mass (probably estimated to about
1 s) and
your mass (probably estimated to about 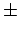 1-2 kg,
including clothes etc.).
In the latter category is your efficiency
1-2 kg,
including clothes etc.).
In the latter category is your efficiency 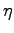 ,
which you had to guess in order to convert
P into
,
which you had to guess in order to convert
P into 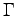 , and your resting metabolism
, and your resting metabolism 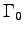 ,
which you had to assume could be estimated from
the "mouse-to-elephant" allometric relation,
,
which you had to assume could be estimated from
the "mouse-to-elephant" allometric relation,
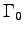 [W] = 4 M[kg]0.75 - which we know is
not a precise law but merely a consistent trend,
with typical deviations of about a factor of two!
A similar "slop" can be expected for the efficiency,
which is only "typically" 25%.
So you should not be expect these calculations to yield
"true" values of your activity factor, were you to
measure same more directly using oxygen consumption etc.
As with all estimations of uncertainty, a good deal of
subjective judgement is necessary;
just be sure you can explain why
you give the estimate you do.
Compound table for those who submitted data:
[W] = 4 M[kg]0.75 - which we know is
not a precise law but merely a consistent trend,
with typical deviations of about a factor of two!
A similar "slop" can be expected for the efficiency,
which is only "typically" 25%.
So you should not be expect these calculations to yield
"true" values of your activity factor, were you to
measure same more directly using oxygen consumption etc.
As with all estimations of uncertainty, a good deal of
subjective judgement is necessary;
just be sure you can explain why
you give the estimate you do.
Compound table for those who submitted data: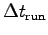 [s]
[s]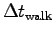 [s]
[s]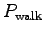 ,
, 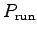 ,
,
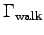 ,
,
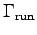 ,
,
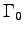 and
and 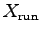 as functions of body mass M.
ANSWER:
This part will also be different for each group.
as functions of body mass M.
ANSWER:
This part will also be different for each group.
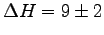 kcal.
What is the [sugar and]12 honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
ANSWER:
Let's treat nectar as a solution of honey in water.
The specific heat of combustion of glucose is hg= 4.15 kcal/g,
so the specific heat of combustion of honey is
kcal.
What is the [sugar and]12 honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
ANSWER:
Let's treat nectar as a solution of honey in water.
The specific heat of combustion of glucose is hg= 4.15 kcal/g,
so the specific heat of combustion of honey is
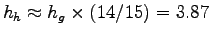 kcal/g.
kcal/g.
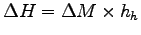 so
so
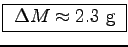 .
.
 of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
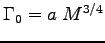 is applicable,
determine the constant a in that rate function.
ANSWER:
Basal metabolic rate scales as
is applicable,
determine the constant a in that rate function.
ANSWER:
Basal metabolic rate scales as
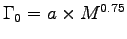 ;
the average daily metabolic rate for the hummingbird
can be expressed as
;
the average daily metabolic rate for the hummingbird
can be expressed as
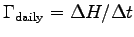 and therefore
and therefore
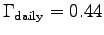 W.
using 4185 J/kcal with
W.
using 4185 J/kcal with
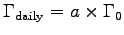 and
and
 kg, we find
kg, we find 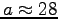 .
Therefore
.
Therefore
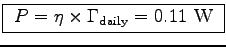 ,
using again
,
using again
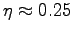 .
.
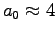 of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
ANSWER:
of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
ANSWER:
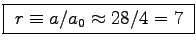 .
.
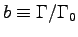 refers to the
refers to the 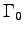 for that animal, so r is not b.
for that animal, so r is not b.
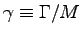 for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
ANSWER:
The specific metabolic rate for the hummingbird is
for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
ANSWER:
The specific metabolic rate for the hummingbird is
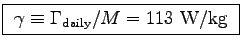 .
For an elephant, assuming M = 5000 kg and
.
For an elephant, assuming M = 5000 kg and
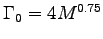 ,
,
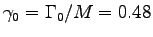 W/kg at rest,
which even with an activity factor of b = 10
would not get higher then roughly
W/kg at rest,
which even with an activity factor of b = 10
would not get higher then roughly
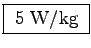 .
Pound for pound, the elephant utilizes energy far more efficiently.
.
Pound for pound, the elephant utilizes energy far more efficiently.
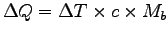 .
The specific heat of tissue is about that of water:
.
The specific heat of tissue is about that of water:
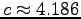 kJ kg-1 K-1.
Thus with
kJ kg-1 K-1.
Thus with
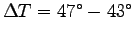 C
C 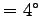 C
and
C
and
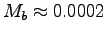 kg, we have
kg, we have
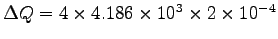 or
or
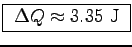 .
.
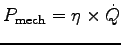 .
The specific muscle power
.
The specific muscle power
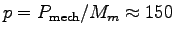 W/kg,
and so if
W/kg,
and so if
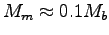 , with Mb = 0.0002 kg we get
the bee's muscle weight
, with Mb = 0.0002 kg we get
the bee's muscle weight
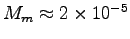 kg,
giving a muscle power
kg,
giving a muscle power
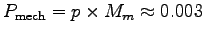 W.
Thus
W.
Thus
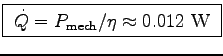 .
.
 with
with
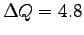 J.
Again,
J.
Again,
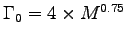 and since
and since
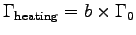 , b = 15
gives
, b = 15
gives
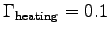 W. Thus
W. Thus
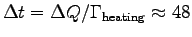 s
or
s
or
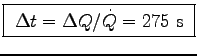 .
.
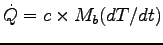 ; in this case,
0.012 W = 4.186 J/kg x 0.0002 kg
x (dT/dt)
giving
; in this case,
0.012 W = 4.186 J/kg x 0.0002 kg
x (dT/dt)
giving
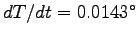 C/s. Thus
C/s. Thus
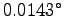 C/s
C/s
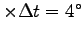 C
implies
C
implies
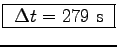 .
.