THE UNIVERSITY OF BRITISH COLUMBIA
 
BIOL/PHYS 438 Assignment # 3:
 
FLUID MECHANICS & LOCOMOTION
 
Tue. 06 Feb. 2007 - finish by Thu. 15 Feb.
Please hand in one assignment per group and list the names & Email addresses of all group members at the top of each sheet.

In general, if you think some necessary information is missing, make a reasonable assumption. But always write down what that assumption is.

Always estimate your uncertainty in any measured quantity, and don't forget to specify all units.

If possible, justify your input. For original comments you may score bonus points!

  1. NEAR SURFACE DRAG: (project by Natasha Szucs, April 2002) Natasha, a good swimmer, wants to quantify the effect of near surface drag. For that purpose she swims with the dolphin kick at various depths y under the water surface. She maintains a constant depth by watching a horizontal line on the pool wall. For every length she swims she measures her travel time with a stopwatch on her wrist.1 The UBC pool is slightly shorter below a depth of 1.50 m (see $\Delta x$ in table below). She also measures her pulse rate Fh, and only uses runs where it stays close to the same value, 140 beats per minute.


     
    Table 1: : Natasha's distance $\Delta x$, elapsed time $\Delta t$ and pulse rate Fh while swimming at depth y under water.
    y [m] $\Delta x$ [m] $\Delta t$ [s] Fh [beats/min] avg. speed [m/s] ratio CDy/CD3
    0 25 26.24 140    
    0 25 26.37 136    
    0.5 25 25.45 140    
    0.5 25 25.15 140    
    1.0 25 23.85 140    
    1.0 25 27.73 140    
    1.5 25 22.95 144    
    1.5 25 22.95 140    
    2.0 22.86 21.90 140    
    2.0 22.86 21.56 144    
    2.5 22.86 21.60 140    
    2.5 22.86 21.44 140    
    3.0 22.86 21.15 136    
    3.0 22.86 21.23 140    

    1. Calculate the average speed for each lap.
    2. Assume a body shape like a flattened torpedo of cross section area A = 0.07 m2, and a drag coefficient CD3 = 0.05 to calculate the average drag force F3 at a depth of y = 3.0 m. This is also the average propulsion force generated by the swimmer.
    3. Since the heart rate is about the same at all depths one can assume that the propulsion force too is the same at all depths. Calculate the drag coefficient ratio CDy/CD3 as function of depth y.
    4. What advice should the UBC coach give to the swimmers?

  2. RED FINGERS: Swirl one arm around as fast as you safely can. Measure the length L of your arm and the time $\Delta t_{10}$ it takes for 10 revolutions, so that you can determine the period $\tau$.

    1. Calculate the average speed of your fingers.
    2. Determine the radial centrifugal acceleration and the additional pressure in the blood vessels in your fingers due to the motion. Compare this pressure to the systolic pressure generated by your heart 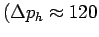$(\Delta p_h \approx 120$ mm Hg), and comment why your fingers are red.

  3. HOW DOES THE FLEA GET YOU? A flea can be modeled as a sphere of 1 mm diameter with a density close to that of water. The flea accelerates at an average rate of 200 g ($\approx 2000$ m/s2), achieving a takeoff velocity that allows it to reach a potential host at h = 0.35 m above ground.

    1. What is the takeoff velocity?
    2. How long is the acceleration phase?
    3. What force is required to obtain this acceleration?
    4. What is the power (force x velocity) at takeoff?
    5. Make a reasonable assumption about the muscle mass involved in a jump and calculate the power requirement per kg of muscle. Given that a typical muscle output is 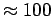$\approx 100$ W/kg, comment on your answer.
    6. Before a jump, the flea stores energy in a pad of resilin, a rubber-like protein built into each hind leg, about 30 µm thick and 80 µm in diameter, with an energy storage capacity of about 1.5 x 106 J/m3. How much potential energy could the flea store in each pad? How long would it take the flea to put that much energy into each pad?


Jess H. Brewer