- Determine the mechanical power output3
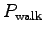 for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
for each team member4 walking up four flights of stairs
(four floors) in the Hebb building.
The height of one "floor" in the Hebb staircase is h = 7.28 m;
if you do the exercise anywhere else you must measure h.
By the definition of the mechanical efficiency
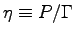 , we have
, we have
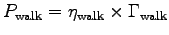 where
where
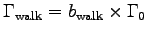 is the metabolic rate while walking up the stairs
and
is the metabolic rate while walking up the stairs
and 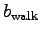 is the corresponding metabolic activity factor.
Calculate
is the corresponding metabolic activity factor.
Calculate
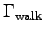 and
and 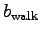 for each team member.
What value should you take for
for each team member.
What value should you take for 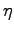 ? Discuss this choice
and comment upon its validity in your written report.
? Discuss this choice
and comment upon its validity in your written report.
- Estimate your uncertainty in this measurement.5 The largest possible value,
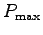 , is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time
, is found by
combining the largest likely value of your body mass,
M+,6 and the shortest possible time 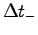 .
Similarly combine the lowest likely body mass M-
and the longest likely time
.
Similarly combine the lowest likely body mass M-
and the longest likely time 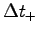 to find a value for
to find a value for 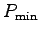 .
A good estimate of the uncertainty in your experimental result
is thus
.
A good estimate of the uncertainty in your experimental result
is thus
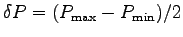 .
Express your answer for the power
.
Express your answer for the power 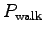 in the form
in the form
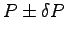 W. (Always include units.)
W. (Always include units.)
- Determine
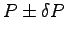 for each one of your team members
when running up the stairs.7
for each one of your team members
when running up the stairs.7
- Estimate the mass of the muscles
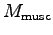 used for running up the stairs and give the power to mass ratio
used for running up the stairs and give the power to mass ratio
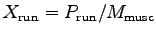 of these muscles.8 Muscle mass (
of these muscles.8 Muscle mass (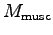 ) = muscle volume (
) = muscle volume (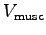 )
times muscle density (
)
times muscle density (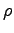 ).
Muscles have about the same density as water.
).
Muscles have about the same density as water.
- Make a table including all your data showing
Name, M,
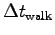 ,
, 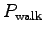 ,
,
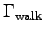 ,
,
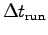 ,
, 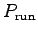 ,
,
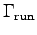 ,
,
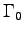 ,
, 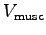 and
and 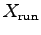 ,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
,
including the uncertainty in each.
Explain your most significant sources of uncertainty.
- Make a log-log graph for each of
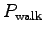 ,
, 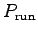 ,
,
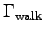 ,
,
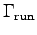 ,
,
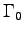 and
and 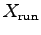 as functions of body mass M.
as functions of body mass M.
The TA will make a compound table for the whole class to get statistical correlations.
- Take an average value of
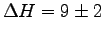 kcal.
What is the sugar and honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
kcal.
What is the sugar and honey content of the nectar?
(Honey has about 14/15 of the heat of combustion of sugar.)
- Determine the metabolic rate
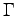 of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
of the little bird,
and estimate its mechanical power output P.
Assuming the metabolic rate function
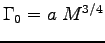 is applicable,
determine the constant a in that rate function.
is applicable,
determine the constant a in that rate function.
- Compare your calculated value of a with
the constant
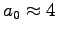 of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
of the mouse to elephant curve
[Eq. (1.5) in the textbook]
and determine the ratio r=a/a0.
Should this ratio be equal to the activity factor b
calculated for the staircase run?
- What problems can you foresee for such a high metabolic rate?
- Calculate the specific metabolic rate
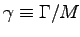 for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
for the hummingbird
and for a 5-ton elephant.
Which animal makes better use of
the energy resources of the environment?
- How much heat energy must be generated by each bee to reach the killing temperature?
- What is the heating power of each bee?
- How quickly do the bees reach the killing temperature?