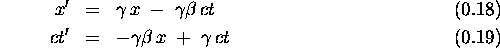
If we now look at just the x and t part of the Lorentz transformation [leaving out the y and z parts, which don't do much anyway], we have
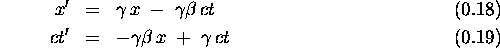
-- , the Lorentz transformation ``sort of'' rotates the space and time axes a little like a normal rotation of x and y. I have used ct as the time axis to keep the units explicitly the same; if we use ``natural units'' (c = 1) then we can just drop c out of the equations completely and the analogy becomes obvious.
Unfortunately, the analogy is flawed.
That extra minus sign in the first equation makes it impossible
to equate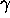 
with the cosine of some
formal angle 
,
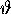since both sin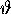
and - sin
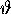would have to be equal to
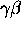(true only in the trivial case
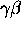= 0,
which is of no interest).
This difference has important consequences which are
best discussed in geometrical terms, which I will get to shortly.
First, however, let me finish describing the part of the analogy
that does work -- and is conceptually very useful!