Next: Chemical Reactions
Up: SPIN
Previous: FERMIONS
Let us consider the consequences of the Pauli exclusion principle
for the chemical properties of atoms: for each allowed wave funtion
(or ``orbital'') of an electron in the Coulomb potential, fully specified
by the quantum numbers 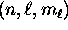 , there are two
(and only two) possible spin states for the electron:
spin ``up'' (
, there are two
(and only two) possible spin states for the electron:
spin ``up'' (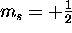 ) and spin ``down'' (
) and spin ``down'' (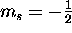 ).
Since the Pauli principle only excludes occupation of exactly
the same state by two electrons, this means that each orbital
may be occupied by at most two electrons;
and if both electrons are present in that orbital,
their spins are necessarily ``paired'' - equal and opposite
in direction, thus perfectly cancelling each other and
contributing nothing to the net angular momentum or magnetic moment.
).
Since the Pauli principle only excludes occupation of exactly
the same state by two electrons, this means that each orbital
may be occupied by at most two electrons;
and if both electrons are present in that orbital,
their spins are necessarily ``paired'' - equal and opposite
in direction, thus perfectly cancelling each other and
contributing nothing to the net angular momentum or magnetic moment.
Determining the chemical properties of the elements thus becomes
a simple matter of counting states: for each ``shell''
(n) we see how many different orbitals there are with different
values of 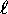 and
and 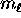 and then multiply by two for the
two
and then multiply by two for the
two 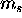 possibilities to get the total number of electrons
that will ``fit'' into that shell. Of course, this simple picture
contains some crude approximations that we must expect to
break down before things get very complicated, and they do.
We assume, for example, that for a positive charge of +Ze
on the nucleus, each time we ``add another electron'' it goes into
the lowest available (unfilled) energy state and effectively
reduces the effective charge of the nucleus by one. That is,
the first electron ``sees'' a positive charge of +Ze but the
second electron ``sees'' a positive charge of
possibilities to get the total number of electrons
that will ``fit'' into that shell. Of course, this simple picture
contains some crude approximations that we must expect to
break down before things get very complicated, and they do.
We assume, for example, that for a positive charge of +Ze
on the nucleus, each time we ``add another electron'' it goes into
the lowest available (unfilled) energy state and effectively
reduces the effective charge of the nucleus by one. That is,
the first electron ``sees'' a positive charge of +Ze but the
second electron ``sees'' a positive charge of 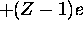 , and so on.
This is not true, of course, for electrons in the same n shell;
they all pretty much see the same apparent charge on the ``core''
of the atom (and see each others' charges as well).
One important effect of such ``screening'' is that states of
higher
, and so on.
This is not true, of course, for electrons in the same n shell;
they all pretty much see the same apparent charge on the ``core''
of the atom (and see each others' charges as well).
One important effect of such ``screening'' is that states of
higher 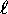 (whose wavefunctions do not penetrate as deeply
into the core) ``see'' on average a lower effective charge
on the core and therefore are slightly less bound (higher energy)
than their low-
(whose wavefunctions do not penetrate as deeply
into the core) ``see'' on average a lower effective charge
on the core and therefore are slightly less bound (higher energy)
than their low-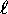 neighbours. This provides the rule that
(up to a point) lower
neighbours. This provides the rule that
(up to a point) lower 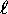 states are filled first.
A collection of states with the same n and
states are filled first.
A collection of states with the same n and 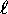 is called a ``subshell.''
is called a ``subshell.''
If we want to do this right for an arbitrary many-electron atom,
we have several very difficult problems to solve:
first, for large Z the innermost electrons
have kinetic energies comparable to their rest mass energy;
thus our nonrelativistic Schr´'odinger equation is inadequate
and one must resort to more advanced descriptions.
Second, the approximation that one shell simply ``screens''
part of the nucleus' charge from the next shell is not that great,
especially for wavefunctions that have a significant probability
density near the nucleus; moreover, electrons in the same
shell definitely ``see'' each other and are affected by that
interaction. One way of approaching this problem is to start
with an initial guess based upon this approximation
and then recalculate each electron wavefunction
including the effects of the other electrons in their wavefunctions;
then go back and correct again with the new guess as a starting point.
Eventually this ``Hartree-Fock'' method should converge on the
actual wavefunctions for all the electrons....
Finally, the coupling of orbital and spin angular momentum
contributions can follow several possible scenarios,
depending upon which couplings are the strongest;
the final result must always be a single overall
net angular momentum (and magnetic moment) for the
atom as a whole; but for large atoms it is very difficult to
predict even its magnitude; the only thing we can be sure of
is that if there are an even number of electrons, protons and
neutrons making up the atom, it will be a boson.
Having issued these caveats, we can go back to our
``state counting'':
- For each ``shell'' characterized by an energy
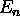 (starting at n = 1, where n is the principle quantum number)
we have n possible values of
(starting at n = 1, where n is the principle quantum number)
we have n possible values of 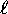 , ranging from
, ranging from 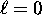 to
to 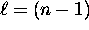 .
.
- For each orbital quantum number
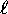 , we have
, we have
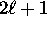 possible values of the magnetic quantum number
possible values of the magnetic quantum number
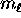 , ranging from
, ranging from 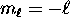 to
to 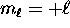 .
.
- For each orbital specified by
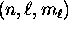 ,
there are two possible values of
,
there are two possible values of 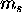 : spin up (
: spin up (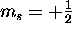 )
and spin down (
)
and spin down (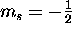 ).
).
Thus there are a total of
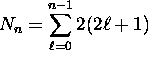 possible fully-specified states for electrons in the
possible fully-specified states for electrons in the 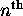 energy shell. For the first shell,
energy shell. For the first shell, 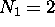 ; for the second shell,
; for the second shell,
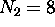 .
.
Since (at least for small n) it is a long way (in energy)
between shells, a ``closed shell'' is especially stable -
it ``likes'' neither to give up an electron nor to acquire
an extra one from another atom; it has ``zero valence.''
This means an atom with 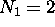 electrons [helium] is
very unreactive chemically, and so is one with
electrons [helium] is
very unreactive chemically, and so is one with 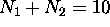 electrons [neon]. This goes on until the breakdown of
our assumption that all the electrons for one shell
are filled in before any electrons from the next shell.
This breakdown comes at the
electrons [neon]. This goes on until the breakdown of
our assumption that all the electrons for one shell
are filled in before any electrons from the next shell.
This breakdown comes at the 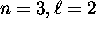 subshell.
subshell.
Section 9.1 of the text provides all the details you need
to explore the periodic table on your own; it also offers
at least a qualitative explanation for the fact that
the 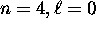 subshell is actually lower in energy
than the
subshell is actually lower in energy
than the 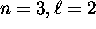 subshell and therefore fills first,
despite having a higher n. This is the point at which
our simple qualitative rules break down and we must rely
on empirical information to further understand the
chemical properties of the elements.
subshell and therefore fills first,
despite having a higher n. This is the point at which
our simple qualitative rules break down and we must rely
on empirical information to further understand the
chemical properties of the elements.
Next: Chemical Reactions
Up: SPIN
Previous: FERMIONS
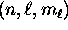 , there are two
(and only two) possible spin states for the electron:
spin ``up'' (
, there are two
(and only two) possible spin states for the electron:
spin ``up'' (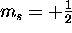 ) and spin ``down'' (
) and spin ``down'' (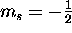 ).
Since the Pauli principle only excludes occupation of exactly
the same state by two electrons, this means that each orbital
may be occupied by at most two electrons;
and if both electrons are present in that orbital,
their spins are necessarily ``paired'' - equal and opposite
in direction, thus perfectly cancelling each other and
contributing nothing to the net angular momentum or magnetic moment.
).
Since the Pauli principle only excludes occupation of exactly
the same state by two electrons, this means that each orbital
may be occupied by at most two electrons;
and if both electrons are present in that orbital,
their spins are necessarily ``paired'' - equal and opposite
in direction, thus perfectly cancelling each other and
contributing nothing to the net angular momentum or magnetic moment.
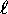 and
and 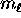 and then multiply by two for the
two
and then multiply by two for the
two 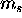 possibilities to get the total number of electrons
that will ``fit'' into that shell. Of course, this simple picture
contains some crude approximations that we must expect to
break down before things get very complicated, and they do.
We assume, for example, that for a positive charge of +Ze
on the nucleus, each time we ``add another electron'' it goes into
the lowest available (unfilled) energy state and effectively
reduces the effective charge of the nucleus by one. That is,
the first electron ``sees'' a positive charge of +Ze but the
second electron ``sees'' a positive charge of
possibilities to get the total number of electrons
that will ``fit'' into that shell. Of course, this simple picture
contains some crude approximations that we must expect to
break down before things get very complicated, and they do.
We assume, for example, that for a positive charge of +Ze
on the nucleus, each time we ``add another electron'' it goes into
the lowest available (unfilled) energy state and effectively
reduces the effective charge of the nucleus by one. That is,
the first electron ``sees'' a positive charge of +Ze but the
second electron ``sees'' a positive charge of 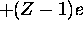 , and so on.
This is not true, of course, for electrons in the same n shell;
they all pretty much see the same apparent charge on the ``core''
of the atom (and see each others' charges as well).
One important effect of such ``screening'' is that states of
higher
, and so on.
This is not true, of course, for electrons in the same n shell;
they all pretty much see the same apparent charge on the ``core''
of the atom (and see each others' charges as well).
One important effect of such ``screening'' is that states of
higher 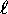 (whose wavefunctions do not penetrate as deeply
into the core) ``see'' on average a lower effective charge
on the core and therefore are slightly less bound (higher energy)
than their low-
(whose wavefunctions do not penetrate as deeply
into the core) ``see'' on average a lower effective charge
on the core and therefore are slightly less bound (higher energy)
than their low-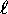 neighbours. This provides the rule that
(up to a point) lower
neighbours. This provides the rule that
(up to a point) lower 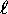 states are filled first.
A collection of states with the same n and
states are filled first.
A collection of states with the same n and 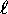 is called a ``subshell.''
is called a ``subshell.''
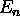 (starting at n = 1, where n is the principle quantum number)
we have n possible values of
(starting at n = 1, where n is the principle quantum number)
we have n possible values of 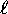 , ranging from
, ranging from 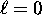 to
to 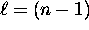 .
.
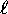 , we have
, we have
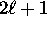 possible values of the magnetic quantum number
possible values of the magnetic quantum number
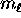 , ranging from
, ranging from 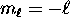 to
to 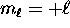 .
.
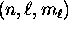 ,
there are two possible values of
,
there are two possible values of 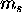 : spin up (
: spin up (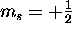 )
and spin down (
)
and spin down (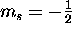 ).
).
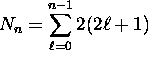 possible fully-specified states for electrons in the
possible fully-specified states for electrons in the 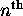 energy shell. For the first shell,
energy shell. For the first shell, 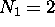 ; for the second shell,
; for the second shell,
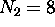 .
.
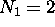 electrons [helium] is
very unreactive chemically, and so is one with
electrons [helium] is
very unreactive chemically, and so is one with 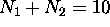 electrons [neon]. This goes on until the breakdown of
our assumption that all the electrons for one shell
are filled in before any electrons from the next shell.
This breakdown comes at the
electrons [neon]. This goes on until the breakdown of
our assumption that all the electrons for one shell
are filled in before any electrons from the next shell.
This breakdown comes at the 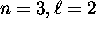 subshell.
subshell.
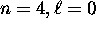 subshell is actually lower in energy
than the
subshell is actually lower in energy
than the 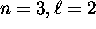 subshell and therefore fills first,
despite having a higher n. This is the point at which
our simple qualitative rules break down and we must rely
on empirical information to further understand the
chemical properties of the elements.
subshell and therefore fills first,
despite having a higher n. This is the point at which
our simple qualitative rules break down and we must rely
on empirical information to further understand the
chemical properties of the elements.