Next: Identical Particles: the
Up: SPIN
Previous: Magnetic Interactions
The following description is bogus. That it, this is not ``really''
what intrinsic angular momentum is all about; but it is possible
to understand it in ``common sense'' terms, so we can use it as a
mnemonic technique. Many concepts are introduced this
sort of ``cheating'' until students get comfortable enough with them
to define them rigourously. (The truth about spin, like much
of QM, can never be made to seem sensible; it can only be gotten
used to!)
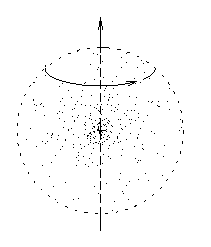 Imagine a big fuzzy ball of mass spinning about an axis.
While you're at it, imagine some electric charge sprinkled in,
a certain amount of charge for every little bit of mass.
(If you like, you can think of a cloud of particles,
each of which has the same charge-to-mass ratio,
all orbiting about a common axis.)
Each little mass element contributes a bit of angular momentum
and a proportional bit of magnetic moment, so that
Imagine a big fuzzy ball of mass spinning about an axis.
While you're at it, imagine some electric charge sprinkled in,
a certain amount of charge for every little bit of mass.
(If you like, you can think of a cloud of particles,
each of which has the same charge-to-mass ratio,
all orbiting about a common axis.)
Each little mass element contributes a bit of angular momentum
and a proportional bit of magnetic moment, so that
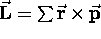 (summed over all the mass elements) and, as for a single
particle,
(summed over all the mass elements) and, as for a single
particle, 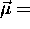 (constant)
(constant)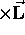 .
If the charge-to-mass ratio happens to be the same as for
an electron, then (constant)
.
If the charge-to-mass ratio happens to be the same as for
an electron, then (constant)
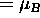 ,
the Bohr magneton.
,
the Bohr magneton.
Now imagine that, like a figure skater pulling in her/his arms
to spin faster, the little bits of charge and mass collapse
together, making r smaller everywhere. To conserve
angular momentum (which is always conserved!)
the momentum p has to get bigger - the bits must spin faster.
The relationship between L and
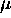 is such that
is such that 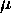 also remains constant as this happens.
also remains constant as this happens.
Eventually the constituents can shrink down to a point
spinning infinitely fast. Obviously we get into a bit of
trouble here with both relativity and quantum mechanics;
nevertheless, this is (sort of) how we think (privately) of
an electron: although we have never been able to find
any evidence for ``bits'' within an electron, we are able to
rationalize its possession of an irreducible, intrinsic
angular momentum (or ``spin'') in this way.
Such intrinsic angular momentum is a property
of the particle itself as well as a dynamical variable
that behaves just like orbital angular momentum.
It is given a special label (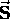 instead of
instead of  )
just to emphasize its difference.
Like
)
just to emphasize its difference.
Like  , it is
quantized - i.e. it only
comes integer multiples of a fundamental quantum of
intrinsic angular momentum - but (here comes the weird part!)
that quantum can be either
, it is
quantized - i.e. it only
comes integer multiples of a fundamental quantum of
intrinsic angular momentum - but (here comes the weird part!)
that quantum can be either 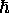 ,
as for
,
as for  ,
or
,
or 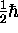 !
!
In the following, s is the ``spin quantum number''
analogous to the ``orbital quantum number''
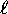 such that the spin angular momentum
such that the spin angular momentum
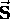 has a magnitude
has a magnitude 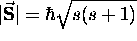 \
and a z component
\
and a z component 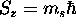 where
where 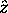 is the chosen spin quantization axis.
The magnetic quantum number for spin
is the chosen spin quantization axis.
The magnetic quantum number for spin
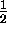 has only two possible values, spin ``up''
(
has only two possible values, spin ``up''
(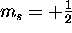 ) and spin ``down''
(
) and spin ``down''
(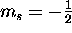 ).
This is the explanation of the Stern-Gerlach result
for silver atoms: with no orbital angular momentum
at all, the Ag atoms have a single ``extra'' electron
whose spin determines their overall angular momentum
and magnetic moment.
).
This is the explanation of the Stern-Gerlach result
for silver atoms: with no orbital angular momentum
at all, the Ag atoms have a single ``extra'' electron
whose spin determines their overall angular momentum
and magnetic moment.
Next: Identical Particles: the
Up: SPIN
Previous: Magnetic Interactions
 Imagine a big fuzzy ball of mass spinning about an axis.
While you're at it, imagine some electric charge sprinkled in,
a certain amount of charge for every little bit of mass.
(If you like, you can think of a cloud of particles,
each of which has the same charge-to-mass ratio,
all orbiting about a common axis.)
Each little mass element contributes a bit of angular momentum
and a proportional bit of magnetic moment, so that
Imagine a big fuzzy ball of mass spinning about an axis.
While you're at it, imagine some electric charge sprinkled in,
a certain amount of charge for every little bit of mass.
(If you like, you can think of a cloud of particles,
each of which has the same charge-to-mass ratio,
all orbiting about a common axis.)
Each little mass element contributes a bit of angular momentum
and a proportional bit of magnetic moment, so that
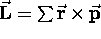 (summed over all the mass elements) and, as for a single
particle,
(summed over all the mass elements) and, as for a single
particle, 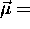 (constant)
(constant)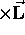 .
If the charge-to-mass ratio happens to be the same as for
an electron, then (constant)
.
If the charge-to-mass ratio happens to be the same as for
an electron, then (constant)
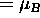 ,
the Bohr magneton.
,
the Bohr magneton.
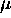 is such that
is such that 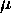 also remains constant as this happens.
also remains constant as this happens.
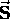 instead of
instead of  )
just to emphasize its difference.
Like
)
just to emphasize its difference.
Like  , it is
quantized - i.e. it only
comes integer multiples of a fundamental quantum of
intrinsic angular momentum - but (here comes the weird part!)
that quantum can be either
, it is
quantized - i.e. it only
comes integer multiples of a fundamental quantum of
intrinsic angular momentum - but (here comes the weird part!)
that quantum can be either 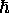 ,
as for
,
as for  ,
or
,
or 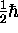 !
!
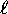 such that the spin angular momentum
such that the spin angular momentum
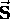 has a magnitude
has a magnitude 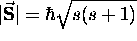 \
and a z component
\
and a z component 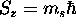 where
where 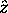 is the chosen spin quantization axis.
The magnetic quantum number for spin
is the chosen spin quantization axis.
The magnetic quantum number for spin
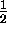 has only two possible values, spin ``up''
(
has only two possible values, spin ``up''
(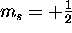 ) and spin ``down''
(
) and spin ``down''
(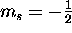 ).
This is the explanation of the Stern-Gerlach result
for silver atoms: with no orbital angular momentum
at all, the Ag atoms have a single ``extra'' electron
whose spin determines their overall angular momentum
and magnetic moment.
).
This is the explanation of the Stern-Gerlach result
for silver atoms: with no orbital angular momentum
at all, the Ag atoms have a single ``extra'' electron
whose spin determines their overall angular momentum
and magnetic moment.