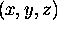 ;
the concept of ``taking partial derivatives'' is independent
of what function we are taking the derivatives of.
It is therefore practical to learn to think of
;
the concept of ``taking partial derivatives'' is independent
of what function we are taking the derivatives of.
It is therefore practical to learn to think of
The foregoing description applies for any function of 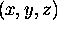 ;
the concept of ``taking partial derivatives'' is independent
of what function we are taking the derivatives of.
It is therefore practical to learn to think of
;
the concept of ``taking partial derivatives'' is independent
of what function we are taking the derivatives of.
It is therefore practical to learn to think of
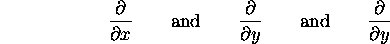
as operators that can be applied to any function
(like F). Put the operator on the left of a function,
perform the operation and you get a partial derivative ---
a new function of 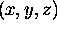 .
In general, such ``operators'' change one function into another.
Physics is loaded with operators like these.
.
In general, such ``operators'' change one function into another.
Physics is loaded with operators like these.
The gradient operator is a vector operator,
written  and called ``del.'' It is
defined as
and called ``del.'' It is
defined as
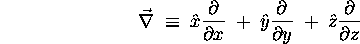
and can be applied directly to any scalar function
of 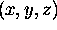 --- say,
--- say, 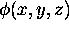 --- to turn it into a
vector function,
--- to turn it into a
vector function, 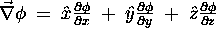 .
.