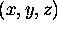 to be
the path of a ray of light. We call this path
a geodesic of space for an important reason
that is best explained by analogy [like most topics in Relativity].
to be
the path of a ray of light. We call this path
a geodesic of space for an important reason
that is best explained by analogy [like most topics in Relativity].


If we want to do geometry, the first thing we need is a
straightedge. Any straight line will do. What shall we use?
Well, modern surveyors are mighty fond of lasers for the
simple reason that light travels in a straight line.
(If light doesn't, what does?!) At least in empty space this
must be true. So if we like we can define a
``straight line'' in 3-space 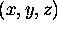 to be
the path of a ray of light. We call this path
a geodesic of space for an important reason
that is best explained by analogy [like most topics in Relativity].
to be
the path of a ray of light. We call this path
a geodesic of space for an important reason
that is best explained by analogy [like most topics in Relativity].
Consider air travel on Earth. Most intercontinental flights take routes called ``great circles'' which may go over the North Pole This is because these are the shortest paths between two points on the Earth, subject to the constraint that one must travel essentially in two dimensions along the surface of the Earth. Such lines, the shortest distances between points subject to the constraint that you must travel along a certain surface, are in general called geodesics, and now we begin to see the connection.
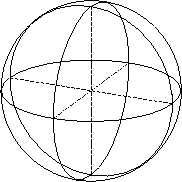
Figure:
``Great circle'' routes on the Earth are geodesics
of the Earth's surface (a 2-D hypersurface embedded
in 3-D space); geometrical figures drawn on this
hypersurface
do not obey Euclidian geometry!
When we wander around the Earth's surface like ``bugs on a balloon,'' we imagine that [neglecting the odd bump here and there] we live in a 2-D space (North-South and East-West). In fact, we are simply restricted by practical considerations to a 2-D surface [within a few miles of altitude] `` embedded '' in a 3-D space. The analogous situation can arise for a 3-D hypersurface embedded in a 4-D space-time continuum. Such a hypersurface contains the geodesics along which light travels.