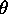we have an argument 
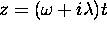where
,
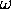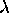and t are all real. Then
What happens if we take the exponential of a quantity that is
neither pure real nor pure imaginary, but a little of both?
We can do this several ways, but in view of our interest in
waves I will put it this way: suppose that instead of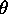
we have an argument 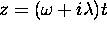where
,
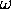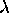and t are all real. Then
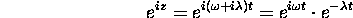
That is, we have an oscillatory function multiplied by an exponentially decaying ``envelope'' function - the phenomenon of damped oscillations that describes virtually every actual case of oscillatory motion.
Another question arises if we are familiar with the hyperbolic functions
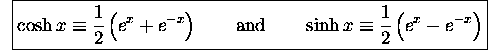
These are so similar to the definitions of the
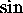and
in terms of complex exponentials that we suspect a connection
between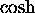 
and
that is deeper than just the fact
that the names are so similar (which should of course have
made us suspicious in the first place). I will leave it as
a (trivial) exercise to show that
