- . . . system?1
- There must be a limit to the amount of energy
the system can hold, otherwise more energy is bound to offer
more possibilities for redistribution, and thus more entropy.
If the entropy is decreasing with increasing energy
(i.e. the derivative is negative)
then by definition the temperature is negative
(i.e. hotter than infinite temperature.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . zero.
2
- There is only one point where the electric field is zero:
exactly as far to the right of the negative charge as the separation
between the charges.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . temperature.3
- The probability of a given single particle state of a given energy
being occupied is the same for both, but the density of states
(i.e. the number of possible states with speeds within a given
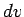 of
of 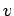 ) is different because there are more directions
for the vector velocity to point in 3 dimensions than in 1 dimension.
You can also describe this in terms of modes of standing waves, but
the classical explanation is adequate for full credit.
) is different because there are more directions
for the vector velocity to point in 3 dimensions than in 1 dimension.
You can also describe this in terms of modes of standing waves, but
the classical explanation is adequate for full credit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . sentences:4
- The electric field inside the tube (
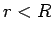 )
is a complicated function of the charge's position.
The electric field outside the tube (
)
is a complicated function of the charge's position.
The electric field outside the tube (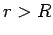 )
has a magnitude
)
has a magnitude
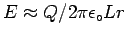 (except near the ends) and is in the
(except near the ends) and is in the
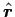 direction.
This is because a net charge
direction.
This is because a net charge 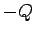 is distributed over the
inside of the conductor in such a (complicated) way as to
terminate all the electric field lines emitted by the point
charge so that the field can be zero inside the conductor,
leaving an equal positive charge
is distributed over the
inside of the conductor in such a (complicated) way as to
terminate all the electric field lines emitted by the point
charge so that the field can be zero inside the conductor,
leaving an equal positive charge 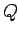 to be distributed
uniformly over the outer surface of the conductor.
So an observer at
to be distributed
uniformly over the outer surface of the conductor.
So an observer at 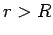 "sees" a uniformly charged
cylinder with a net charge per unit length of
"sees" a uniformly charged
cylinder with a net charge per unit length of 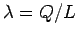 ,
producing an electric field
,
producing an electric field
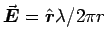 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . charge?5
- To the left of the positive sheet of charge
and to the right of the negative sheet of charge,
the electric field is zero, because a Gaussian "pillbox" surface
cutting through the entire array at right angles encloses no net charge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . slab?6
- A negative surface charge is attracted to the left side
of the conductor by the positive sheet of charge, leaving behind
an equal and opposite positive surface charge on the right side.
These induced surface charges must cancel the electric fields
of the sheets inside the conductor, so they produce electric
fields of their own with the same magnitude as those of the sheets,
and (between the sheets and the conductor) in the same direction.
So in both gaps we get an electric field to the right
whose (uniform) magnitude is
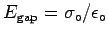 ,
twice that from a single sheet,
,
twice that from a single sheet,
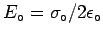 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . slab?7
- The electric field inside any conductor is zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . .
8
- There are several ways to think about this question;
the trick is not to get them mixed up. The reasoning given in
the answer to the previous question treats all sheets of charge
(original or induced) on an equal basis, explaining the zero
electric field within the conductor explicitly in terms of
the sum of several contributions. This immediately gives
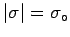 on both sides of the slab.
You can also use the general rule (obtained by taking a
very small Gaussian "pillbox" that only encloses one surface
of the conductor) that
on both sides of the slab.
You can also use the general rule (obtained by taking a
very small Gaussian "pillbox" that only encloses one surface
of the conductor) that
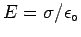 near the
surface of any conductor; in this case
near the
surface of any conductor; in this case
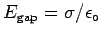 but since
but since
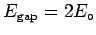 and
and
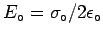 we get
we get
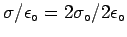 or
or
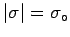 again.
again.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain.
9
- Zero . There is no net charge enclosed within
a coaxial Gaussian cylinder of radius
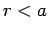 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain.
10
- Zero . There is a positive charge
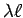 from the inner conductor and a negative charge
from the inner conductor and a negative charge 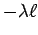 from the outer conductor both enclosed within
a coaxial Gaussian cylinder of length
from the outer conductor both enclosed within
a coaxial Gaussian cylinder of length 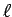 and radius
and radius 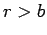 ,
but there is still no net charge enclosed.
,
but there is still no net charge enclosed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?
11
- Now it gets interesting. A coaxial Gaussian cylinder
of length
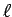 and radius
and radius 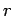 between
between 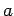 and
and 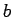 encloses a
net positive charge
encloses a
net positive charge
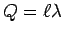 which must equal
which must equal
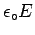 times the surface area
times the surface area 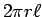 through which
through which
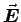 emerges, giving the familiar
emerges, giving the familiar
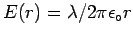 .
The negative shell of charge at
.
The negative shell of charge at 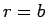 is not enclosed,
so it contributes nothing to
is not enclosed,
so it contributes nothing to 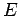 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ?
12
- You are welcome to do an integral if you wish, but I
excused you from this chore by specifying that you can treat
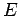 as constant in the narrow gap, giving simply
as constant in the narrow gap, giving simply
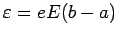 .
Check the sign: the negatively charged electron experiences an
inward force so "out" is "uphill" and
.
Check the sign: the negatively charged electron experiences an
inward force so "out" is "uphill" and
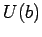 is greater than
is greater than 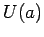 .
With
.
With
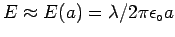 this gives
this gives
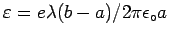 .
Putting in the numbers gives
.
Putting in the numbers gives
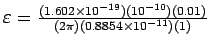 or
or
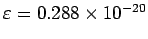 J .
J .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . surface?13
- Here we have two states of different energies
and therefore different Boltzmann factors. If we define
the energy of a bead stuck to the surface at
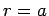 to be zero, then the ratio of
the probability
to be zero, then the ratio of
the probability 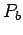 of being stuck to the surface at
of being stuck to the surface at 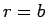 to
the probability
to
the probability 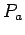 of being stuck to the surface at
of being stuck to the surface at 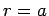 is
is
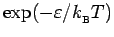 , where
, where 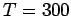 K
and
K
and
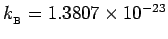 J/K, giving
J/K, giving
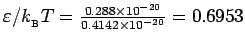 and
and
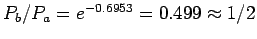 .
Since
.
Since
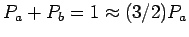 ,
,
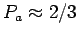 and
and
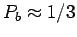 , so on average 67 of the 100 beads
will be stuck to the surface at
, so on average 67 of the 100 beads
will be stuck to the surface at 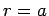 and 33
will be stuck to the surface at
and 33
will be stuck to the surface at 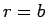 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.