- (a)
-
An electric field of 100 V/m acts between two
parallel capacitor plates separated by an air gap.
Without altering the charge on either plate,
we now completely fill the space between the plates with
strontium titanate, whose dielectric constant is
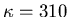 .
What is then the electric field between the plates?
1
.
What is then the electric field between the plates?
1
- (b)
-
Two resistors have a net resistance of
16
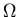 when connected in series and
3
when connected in series and
3 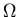 when connected in parallel.
What are their individual resistances?
2
when connected in parallel.
What are their individual resistances?
2
- (c)
-
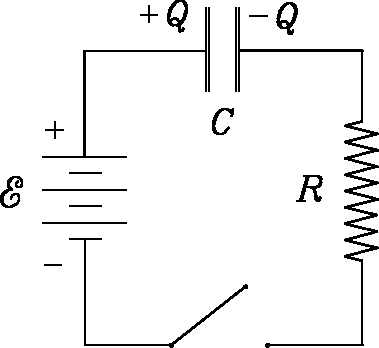
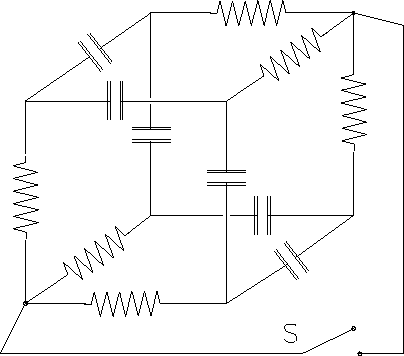
Six identical capacitors of capacitance C=1 F
and six identical resistors of resistance
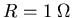 are arranged in a cube as shown.
Before it is closed at t=0, there is a potential
of 1 V across the switch S.
are arranged in a cube as shown.
Before it is closed at t=0, there is a potential
of 1 V across the switch S.
- i.
- [4 marks] What is the net charge stored in the circuit before the switch is closed? 3
- ii.
- [4 marks]
How long will it take for the net charge on any capacitor
to drop to 1/e of its initial value? [
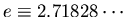 ]
4
]
4
- iii.
- [2 marks] Would there be an unique answer to the previous question if one of the capacitors had a different capacitance from the others? Explain. 5
- (d)
-
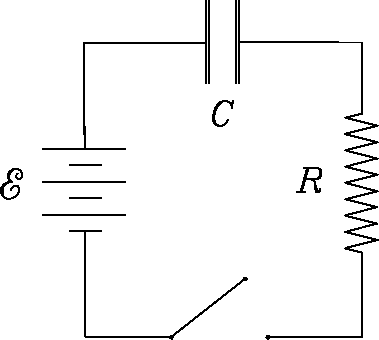
Describe in detail what happens when the switch is closed at t=0
in each of the following circuits, where in each case
C = 0.1 F,
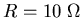 and
and
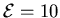 V.
V.
- (e)
-
A velocity selector has a magnetic field
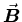 perpendicular to an electric field of 30,000 V/m.
Charged particles with velocity
perpendicular to an electric field of 30,000 V/m.
Charged particles with velocity
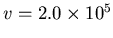 m/s
move through the device undeflected.
What is the strength of
m/s
move through the device undeflected.
What is the strength of
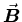 [in Tesla]?
8
[in Tesla]?
8
- (f)
-
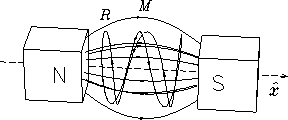
A proton is trapped in a magnetic mirror system as shown.
In its spiraling motion, the proton's total kinetic energy
and the magnetic flux encircled by its orbit both remain constant.
Explain why the total kinetic energy of the proton remains constant.
9
- (a)
- [5 marks]
In what direction is the vector magnetic field
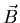 in various regions?
(Indicate on the sketch and/or in words.)
10
in various regions?
(Indicate on the sketch and/or in words.)
10
- (b)
- [10 marks] Find a complete expression for the magnetic field strength B as a function of r (the distance from the central axis), I and R. 11
- (c)
- [5 marks] Plot B(r) from r=0 to r=2R, labeling your axes clearly (including the vertical scale in Tesla and the horizontal scale in meters). 12
Many people solved a different problem, usually an adaptation of the homework problem in which the current is uniformly distributed over a solid cylindrical conductor. Others failed to recognize that the same current flows up the central wire in one direction and back down the outer shell in the opposite direction. Still others thought the outer shell was not for the full length of the wire. I suppose I should take greater care in the wording of the question, but it is important to ask if you are confused about the terms of reference. I may not answer all your questions, but I will be glad to resolve unintended ambiguities.