- (a)
-
In the homework problem on "Stat Ec", a "system" of N shares
of a stock worth
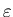 each has n shares bought,
resulting in a net investment of
each has n shares bought,
resulting in a net investment of
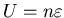 in that stock.
(Both
in that stock.
(Both
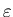 and U are measured in monetary units.)
If we define the entropy
of such a system as
the log of the number of different ways n shares could be sold,
and the economic temperature
of the system in the
usual way as the inverse of
the rate of change of the entropy with respect to U
(i.e. the slope of the curve of entropy as a function of U),
then
and U are measured in monetary units.)
If we define the entropy
of such a system as
the log of the number of different ways n shares could be sold,
and the economic temperature
of the system in the
usual way as the inverse of
the rate of change of the entropy with respect to U
(i.e. the slope of the curve of entropy as a function of U),
then
- i.
- What fraction of the shares will be sold at infinite economic temperature? 1
- ii.
- For what U is the stock "hottest"? 2
- iii.
- Describe the economic temperature of the stock at that U. 3
- (b)
-
For an ideal gas of N particles in thermal equilibrium,
the mean internal energy depends on . . .
[encircle all correct answers] 4
(i) temperature (ii) pressure (iii) volume - (c)
-
To prevent nitrogen bubbles forming in the blood ("the bends"),
divers in high pressure chambers often breathe "heliox",
a mixture of helium gas and oxygen gas.
In a room filled with such a mixture,
what is the ratio of the average speed
of the 4He atoms to that of the 16O2
molecules? 5
- (d)
-
In a hydrogen atom, the electrostatic force between
the proton and electron is
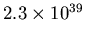 times greater
than the gravitational force.
If we can adjust the distance between the two particles,
at what separation will the electrostatic and gravitational
forces between them be equal?
Explain. 6
times greater
than the gravitational force.
If we can adjust the distance between the two particles,
at what separation will the electrostatic and gravitational
forces between them be equal?
Explain. 6
- (e)
-
An electric dipole,
consisting of a 0.01 C positive electric charge
1 cm away from an equal-magnitude negative charge,
is located at the centre of a sphere of radius 1 m.
What is the average value of the dipole's electric field
normal to the sphere's surface?
Explain. 7
- (f)
-
A finite conducting slab of thickness d
and area
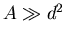 has a charge Q uniformly distributed over its surface.
If the electric field
has a charge Q uniformly distributed over its surface.
If the electric field
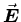 is measured along an axis
normal to the surface and passing near the centre of the slab,
match up all the left and right side phrases
that make up true sentences: 8
is measured along an axis
normal to the surface and passing near the centre of the slab,
match up all the left and right side phrases
that make up true sentences: 8


- (a)
- [5 marks] What is the electric field
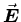 outside the sphere (r > R)? 10
outside the sphere (r > R)? 10
- (b)
- [15 marks] What is the electric field
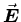 inside the sphere (
inside the sphere (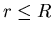 )? 11
)? 11