- . . . B. 1
-
The electric field at point A is in the positive x direction;
the field at point B is in the negative x direction because
the y components of the fields from the two charges cancel by
symmetry, leaving only the x components, which are both negative.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . zero? 2
-
The positive charge is closer, so its (positive) potential exceeds the
negative potential of the negative charge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . B? 3
-
The positive and negative charges are equidistant from B,
so their potentials cancel exactly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
perpendicular? 4
-
This question was on a WebCT Quiz. The electric field
must be perpendicular to the velocity or the particle's speed
would change, altering the magnetic force. The magnetic field
need not be perpendicular to the velocity, as long as it has a
perpendicular component big enough to cancel the electric force.
And therefore the magnetic field need not be perpendicular to the
electric field either.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ? 5
-
The EQUIPARTITION THEOREM states that
in thermal equilibrium at temperature
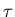 ,
the rms energy associated with any "degree of freedom"
for which positive and negative values yield the same energy
is simply
,
the rms energy associated with any "degree of freedom"
for which positive and negative values yield the same energy
is simply 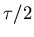 .
The charge on a capacitor is
such a degree of freedom, since the energy stored in the
capacitor is given by Q2/2C. Thus
.
The charge on a capacitor is
such a degree of freedom, since the energy stored in the
capacitor is given by Q2/2C. Thus
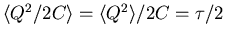 or
or
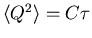 .
Here C = 1 F and
.
Here C = 1 F and
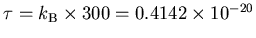 J, giving
J, giving
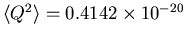 C2 or
C2 or
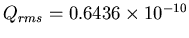 C.
C.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . answer] 6
-
If the wires were parallel the capacitance would be infinite,
but they are perpendicular, so the capacitance is finite.
But calculating it would not be trivial.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain. 7
-
Like the usual lens coating, this one produces a phase shift of
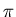 at the first reflection; but unlike the usual low-index
coating, it does not produce any phase shift at the
second reflection. So the two reflected rays will be
out of phase for zero coating thickness -
the ideal nonreflective coating! Now, of course one cannot make
a coating of literally zero thickness, and a coating
half a wavelength thick would also be nonreflective -
for that wavelength! So the ideal thickness
(nonreflective for all visible wavelengths)
would be as close to zero as possible,
or "much thinner than any of the wavelengths of interest".
at the first reflection; but unlike the usual low-index
coating, it does not produce any phase shift at the
second reflection. So the two reflected rays will be
out of phase for zero coating thickness -
the ideal nonreflective coating! Now, of course one cannot make
a coating of literally zero thickness, and a coating
half a wavelength thick would also be nonreflective -
for that wavelength! So the ideal thickness
(nonreflective for all visible wavelengths)
would be as close to zero as possible,
or "much thinner than any of the wavelengths of interest".
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . credit.) 8
-
The temperature is defined as the inverse
of the rate of change of entropy with energy.
In general, this is independent of the absolute magnitude
of either the energy or the entropy.
Although there are some systems in which energy and entropy
both increase with increasing temperature, this is not always true.
Therefore only the next-to-last answer is correct.
The last one would be right if one of the
"increases" were a "decreases"
but the derivative defines 1/T, not T.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . loop? 9
-
Parallel currents attract; antiparallel currents repel.
Thus a segment of wire on one side of the expanded loop
repels one on the other side, causing the loop to expand.
Another way of looking at it is that the coil contains
a region of magnetic field which therefore has a positive
energy density; spreading out to the largest diameter
reduces the energy density, so there is a force
"trying" to increase that diameter.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . loop? 10
-
The magnetic field at the centre of a current loop is inversely
proportional to the radius of the loop; this gives one factor of 1/2.
There are also two turns in the double-loop coil, giving another
factor of 1/2 for a total ratio of 1/4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . true? 11
-
This question was on a WebCT Quiz.
A simple application of Ampère's Law reveals that
there can be no field inside the tube,
since any Ampèrian loop in that region encloses no current;
but the field outside the tube is (by symmetry)
the same as if the current were carried by a wire down its axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . line.) 12
-
Everyone should get this without help; it was provided
partly as a "built in Summary Sheet" of all the
fundamental relationships in Electricity & Magnetism.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . field)? 13
-
Spin up means magnetic moment down; the potential energy of a
magnetic moment in a magnetic field is given by
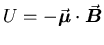 so the spin up state
is the higher energy state for the electron.
The only way for the higher energy state to be
preferentially populated is if the heat reservoir
is at a vanishingly small negative temperature.
(A reservoir of nuclear spins, for instance, could be prepared
at such a temperature by suddenly reversing the magnetic field;
but most "normal" reservoirs can only have positive temperatures,
so an answer of "It's impossible!" is worth 2 out of 3 marks.)
so the spin up state
is the higher energy state for the electron.
The only way for the higher energy state to be
preferentially populated is if the heat reservoir
is at a vanishingly small negative temperature.
(A reservoir of nuclear spins, for instance, could be prepared
at such a temperature by suddenly reversing the magnetic field;
but most "normal" reservoirs can only have positive temperatures,
so an answer of "It's impossible!" is worth 2 out of 3 marks.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . field)? 14
-
This is the lower energy state and therefore its probability
approaches 1 as the temperature approaches zero.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . "down"? 15
-
This would be the situation for infinite temperature
(positive or negative, they amount to the same thing).
Note: this whole question could have been included in the
"QUICKIES" section, as it involves no calculations at all.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . closed. 16
-
The circuit must contain an inductance and a capacitance to oscillate.
To get the prescribed frequency we need
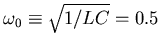 s-1, or LC = 4 s-2. We can get an effective L
of 2 H by connecting the two inductances in series and an effective
C of 2 F by connecting the two capacitors in parallel:
s-1, or LC = 4 s-2. We can get an effective L
of 2 H by connecting the two inductances in series and an effective
C of 2 F by connecting the two capacitors in parallel:
0.75in
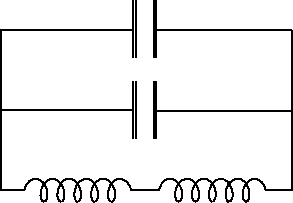
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . =0. 17
-
The initial charge on each capacitor is Q0 = 1 V
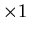 F = 1 C.
The effective resistance is 4
F = 1 C.
The effective resistance is 4 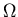 ,
the effective capacitance
is 1/2 F and the effective inductance is 2 H.
You can quickly reproduce the derivation for k
in the trial solution
Q(t) = Q0 ekt:
,
the effective capacitance
is 1/2 F and the effective inductance is 2 H.
You can quickly reproduce the derivation for k
in the trial solution
Q(t) = Q0 ekt:
where
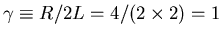 s-1 and
s-1 and
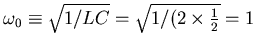 s-1.
Thus
s-1.
Thus
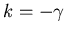 and the charge on each capacitor varies as
and the charge on each capacitor varies as
![\fbox{ $Q(t) = [1$ ~C$] \; \times \exp(-t/1$ ~s) }](img38.gif) .
The current is just the derivative of Q with respect to time:
.
The current is just the derivative of Q with respect to time:
![\fbox{ $I(t) = \dot{Q} = - k Q = - [1$ ~A$] \; \times \exp(-t/1$ ~s) }](img39.gif) .
(The current is negative because the charge is decreasing.)
.
(The current is negative because the charge is decreasing.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . resistor. 18
-
The two rails, the resistor and the bar make a Faraday loop
enclosing a magnetic flux
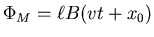 where x0 is the position of the bar at t=0, whenever that was.
It doesn't matter, since to get the induced
where x0 is the position of the bar at t=0, whenever that was.
It doesn't matter, since to get the induced
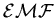 we take
the time derivative:
we take
the time derivative:
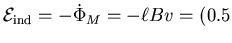 m
m
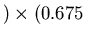 T
T
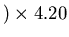 m/s)
or
m/s)
or
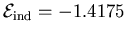 V. This voltage applied across
the resistor gives a current of -0.1181 A, and the product of
the voltage times the current (i.e. the power dissipated
in the resistor) is therefore
P = 0.1674 W.
V. This voltage applied across
the resistor gives a current of -0.1181 A, and the product of
the voltage times the current (i.e. the power dissipated
in the resistor) is therefore
P = 0.1674 W.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . . 19
-
The first minimum of the diffraction pattern
(defining the width of an individual slit) is at about 50 mm or 0.05 m,
which at a distance of 1 m is equivalent to
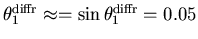 ,
so that the slit width is 1/0.05 = 20 times the wavelength:
,
so that the slit width is 1/0.05 = 20 times the wavelength:
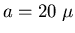 m. The fourth principal maximum of the
intereference pattern appears to be right on top of
the first diffraction mimimum, which means that the
distance between slits is four times the slit width:
m. The fourth principal maximum of the
intereference pattern appears to be right on top of
the first diffraction mimimum, which means that the
distance between slits is four times the slit width:
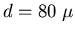 m.
Finally, there are four secondary maxima and five minima
between principal maxima, so there are N = 6 slits.
m.
Finally, there are four secondary maxima and five minima
between principal maxima, so there are N = 6 slits.
2.75in
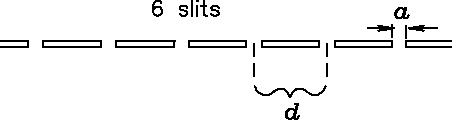
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.



