- . . . possible. 1
-
By thin film interference. If the wing is coated
with a film of higher index of refraction than the wing material
and a thickness equal to one fourth of the wavelength of blue light
(at that index of refraction) then blue light will be preferentially
reflected relative to other colours. If the film has a lower
index than the wing material, the same effect can be achieved if its
thickness is half the wavelength, because in that case
both reflected rays have the same phase reversal so the net
path length difference needs to be a full wavelength.
(I gave full credit for the first sentence of this answer.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . contribution? 2
-
Maxwell proposed the modification of Ampère's Law
by adding the ``displacement current''
(rate of change of the electric flux through the loop)
to the charge-flow current linking the loop.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . represent? 3
-
The speed of light,
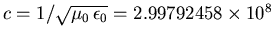 m/s. You can work this out from the
given values of the two constants, but it's a lot quicker to
just remember this important fact.
m/s. You can work this out from the
given values of the two constants, but it's a lot quicker to
just remember this important fact.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . answers] 4
-
The second and fourth answers are correct.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
Explain. 5
-
They can never be equal. Both forces have the same
dependence on distance, so the ratio of their strengths will
always be the same. (This was a trick question designed to
catch people who start calculating before they think.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . given. 6
-
If the plates carry a charge Q then the surface charge density
is
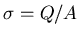 .
The field between the plates would thus be
.
The field between the plates would thus be
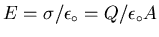 if the gap were empty.
The effect of the dielectric is to reduce E by a factor
if the gap were empty.
The effect of the dielectric is to reduce E by a factor
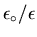 .
Thus in region 1 the field is
.
Thus in region 1 the field is
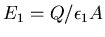 and in region 2 the field is
and in region 2 the field is
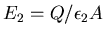 .
Moving from one plate to the other
we travel a distance d/2 along E1
and another distance d/2 along E2
for a net potential change of
.
Moving from one plate to the other
we travel a distance d/2 along E1
and another distance d/2 along E2
for a net potential change of
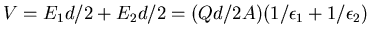 .
Since C is defined by Q = CV or C = Q/V, we have
.
Since C is defined by Q = CV or C = Q/V, we have
![\fbox{ ${\displaystyle C = {2 A \over \left[ {1 \over \epsilon_1}
+ {1 \over \epsilon_2} \right] d } }$\space }](img15.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . coil? 7
-
The resonant frequency of the LC circuit is
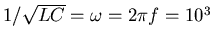 s-1 so
LC = 10-6 s2.
The time constant of the RC circuit is
s-1 so
LC = 10-6 s2.
The time constant of the RC circuit is
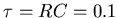 s for
s for
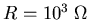 so
103 C =0.1 or
C = 10-4 F [Farads].
Thus
10-4 L = 10-6 or
so
103 C =0.1 or
C = 10-4 F [Farads].
Thus
10-4 L = 10-6 or
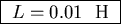 [Henries].
[Henries].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . identical. 8
-
The third circuit is simple because the array of resistors
can be replaced by a single equivalent resistor.
The fourth (rightmost) circuit is obviously not simple
because it has unlike components in parallel;
this can also be seen by picturing what it will ``do''
when the circuit is initially completed.
The second circuit looks topologically suspicious,
and would not be ``simple'' if the elements of the same type
(resistors or capacitors) were not identical;
but since both capacitors must have the same charge at all times
and since the discharge path for each is also identical,
a simple RC circuit with one equivalent capacitor
and one equivalent resistor would have the same behaviour.
The same is true of the first (leftmost) circuit
for the same reasons, although it might be tedious to calculate
the values of the equivalent R and C; in this case
one must have a good eye for symmetry to see that each
corner has three identical resistors in parallel,
each of which collects charge from two identical capacitors.
Again, if the symmetry were broken (e.g. by having one
capacitor or resistor different from the others) the circuit
would no longer be simple.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
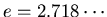 ) 9
) 9
-
Boltzmann showed that the probability a system being in a state of energy
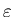 while in thermal equilibrium with a heat reservoir at
temperature
while in thermal equilibrium with a heat reservoir at
temperature 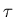 is proportional to
is proportional to
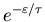 .
For the state with zero energy this is just 1,
so the relative probability of being in the other state
is just
.
For the state with zero energy this is just 1,
so the relative probability of being in the other state
is just
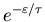 .
If we want this to equal e-1 we must have
.
If we want this to equal e-1 we must have
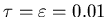 eV
eV
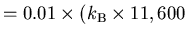 K)
K)
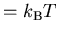 or T = 116 K.
or T = 116 K.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . awake? 10
-
Following the same argument as before, we are looking for
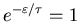 .
This is only true if
.
This is only true if
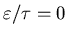 ,
which for finite
,
which for finite
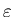 is only true when
is only true when
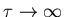 .
You don't really have to do the mathematics to realize this, though,
if you think about what the Boltzmann distribution describes.
Anyone who got stuck on this part ought to have gotten
a good retroactive hint from the graphs in the next part!
.
You don't really have to do the mathematics to realize this, though,
if you think about what the Boltzmann distribution describes.
Anyone who got stuck on this part ought to have gotten
a good retroactive hint from the graphs in the next part!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
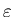 . 11
. 11
-
The probability at
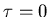 is zero;
it stays ``pretty small'' until it shoots up around
is zero;
it stays ``pretty small'' until it shoots up around
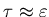 and then slowly approaches 1/2
as
and then slowly approaches 1/2
as
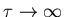 .
Don't forget that factor of 2!
The best you can do it to make it equally probable
to be either asleep or awake. (See previous question.)
.
Don't forget that factor of 2!
The best you can do it to make it equally probable
to be either asleep or awake. (See previous question.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
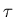 . 12
. 12
-
This is just an exponential decay from 1/2 at
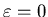 to zero as
to zero as
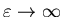 ,
with a value of
,
with a value of
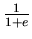 at
at
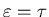 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . axis. 13
-
Imagine a cylindrical Gaussian surface of length L
centred on the same axis, with radius r < R.
The electric field is normal to the curved surface
and has a constant magnitude everywhere on that surface
(by symmetry) so the surface integral in Gauss' Law has the value
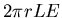 .
The enclosed charge is
.
The enclosed charge is
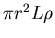 so Gauss' Law gives
so Gauss' Law gives
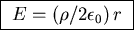 .
QED.
.
QED.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . hole. 14
-
The electric field points away from the axis, so the force on
a (negatively charged) electron points back toward the axis
and has a magnitude proportional to the distance from the axis.
This constitutes a linear restoring force
and the electron has mass (inertia), so
simple harmonic motion is automatic. QED
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain. 15
-
Let r be the radius of the solenoid and d be the width of the wire.
The length of the solenoid is
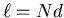 where N is the number of turns.
where N is the number of turns.
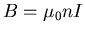 where n = turns/unit length =
where n = turns/unit length =
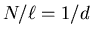 ,
so for a given I, B is independent of the diameter 2r,
as long as there is enough wire to make the solenoid ``long''
(
,
so for a given I, B is independent of the diameter 2r,
as long as there is enough wire to make the solenoid ``long''
(
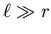 ). Otherwise the Ampère's Law formula for B
will be an overestimate and the true B will be smaller.
Thus a strictly correct answer would be,
``All other things being equal, smaller is slightly better.''
). Otherwise the Ampère's Law formula for B
will be an overestimate and the true B will be smaller.
Thus a strictly correct answer would be,
``All other things being equal, smaller is slightly better.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Explain. 16
-
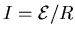 and
and
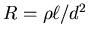 ,
so
,
so
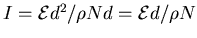 . [1]
But for a given V = L d2
(where L is the total length of the wire)
the number of turns is
. [1]
But for a given V = L d2
(where L is the total length of the wire)
the number of turns is
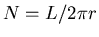 or
or
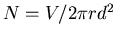 .
Put this back into [1] to get
.
Put this back into [1] to get
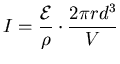 and so
and so
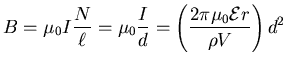 implying that short and thick is lots better,
until you start to have
implying that short and thick is lots better,
until you start to have 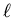 comparable to r,
at which point you eventually reach the point of diminishing returns.
Also, of course, you can't make
comparable to r,
at which point you eventually reach the point of diminishing returns.
Also, of course, you can't make
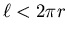 or you won't even be able to make up a single turn!
There is another practical limit to this strategy:
it is actually difficult to produce enormous currents at moderate voltage
because any actual power supply has a resistance of its own,
usually higher than that of a putative single turn of copper bar.
The would-be Electrical Engineer may want to perform a calculation
of the optimum conductor dimensions to generate the maximum B
with the least possible power consumption, given a finite
resistance in the power supply itself . . . .
or you won't even be able to make up a single turn!
There is another practical limit to this strategy:
it is actually difficult to produce enormous currents at moderate voltage
because any actual power supply has a resistance of its own,
usually higher than that of a putative single turn of copper bar.
The would-be Electrical Engineer may want to perform a calculation
of the optimum conductor dimensions to generate the maximum B
with the least possible power consumption, given a finite
resistance in the power supply itself . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . constants.) 17
-
As the bar drops at a speed v, the magnetic flux through the loop
formed by the bar, rails and resistor decreases at a rate
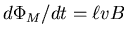 ,
giving an induced EMF V of the same magnitude.
By Lenz' Law this EMF will ``try'' to replace the flux into the page:
a current will be induced in such a direction as to make its own
magnetic field into the page, namely clockwise.
The resulting current will be
,
giving an induced EMF V of the same magnitude.
By Lenz' Law this EMF will ``try'' to replace the flux into the page:
a current will be induced in such a direction as to make its own
magnetic field into the page, namely clockwise.
The resulting current will be
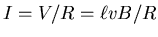 .
A current of this size in a perpendicular magnetic field B
produces a force
.
A current of this size in a perpendicular magnetic field B
produces a force
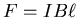 on the bar.
Checking with the right hand rule confirms that the force will be up,
thus counteracting the downward force of gravity.
The magnetic force increases as the velocity increases, until it
exactly balances mg, at which velocity (vt) there is no net force
and terminal velocity will have been reached.
Thus
on the bar.
Checking with the right hand rule confirms that the force will be up,
thus counteracting the downward force of gravity.
The magnetic force increases as the velocity increases, until it
exactly balances mg, at which velocity (vt) there is no net force
and terminal velocity will have been reached.
Thus
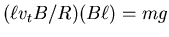 or
or
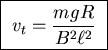 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . side. 18
-
The wide diffraction envelope from the narrow slit width
has a first minimum at
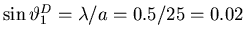 whereas the
whereas the
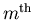 principal maximum of
the interference pattern from the 3 slits
is at
principal maximum of
the interference pattern from the 3 slits
is at
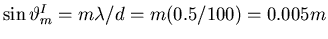 .
The position x on a flat screen 1 m away
is given by
.
The position x on a flat screen 1 m away
is given by
![$x \hbox{\rm [m]} = \tan \vartheta$](img73.gif) .
All the angles are small out to at least
.
All the angles are small out to at least
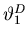 ,
so we can
use the small angle approximations
,
so we can
use the small angle approximations
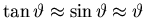 to get
x1D = 0.02 m (2 cm) and
xmI = 0.005 m m (0.5 m cm).
Note that x1D is right on top of x4I and the principal maxima
are evenly spaced. The only other thing you need to remember to get
the full pattern is that for N = 3 slits there are N-1 = 2 minima
and N-2 = 1 secondary maximum between the principal maxima.
The pattern therefore looks like this:
to get
x1D = 0.02 m (2 cm) and
xmI = 0.005 m m (0.5 m cm).
Note that x1D is right on top of x4I and the principal maxima
are evenly spaced. The only other thing you need to remember to get
the full pattern is that for N = 3 slits there are N-1 = 2 minima
and N-2 = 1 secondary maximum between the principal maxima.
The pattern therefore looks like this:
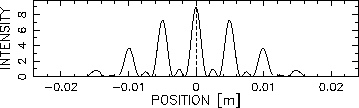
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . maximum. 19
-
For the central maximum (or any principal maximum) the phasor diagram
is three vectors of the same length added tip-to-tail all in the
same direction, so the net amplitude is three times that of each.
When the three individual phasors are perpendicular as shown,
the net amplitude is just the missing side of the square, or
1/3 as big as for the central maximum.
Since the intensity is the square of the amplitude,
this gives 1/9 of the central intensity.
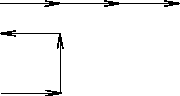
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . maximum? 20
-
Rayleigh's criterion says that two lines are just resolvable
if the principal maximum of one falls right on top of the first
minimum beyond that principal maximum of the other.
A grating gives larger dispersion (change of angle with wavelength)
for higher order principal maxima, but here we are using m=1.
Thus the criterion is that
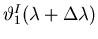 ,
the angle of the first principal maximum for the second wavelength,
is equal to the angle
,
the angle of the first principal maximum for the second wavelength,
is equal to the angle
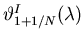 of the first local minimum beyond the first principal maximum
for the original wavelength. That this occurs 1/N = 1/3 of the way
to the second principal maximum can be seen by picturing the
phasor diagram for that first minimum: an equilateral triangle
with each phasor
of the first local minimum beyond the first principal maximum
for the original wavelength. That this occurs 1/N = 1/3 of the way
to the second principal maximum can be seen by picturing the
phasor diagram for that first minimum: an equilateral triangle
with each phasor
 out of phase with the next.
Since
out of phase with the next.
Since
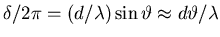 ,
this value of
,
this value of 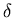 corresponds to
corresponds to
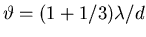 .
At the same angle we have
the first principal maximum (
.
At the same angle we have
the first principal maximum (
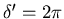 )
for
)
for
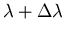 ,
that is,
,
that is,
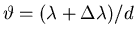 .
Combining these results gives
.
Combining these results gives
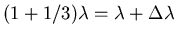 or
or
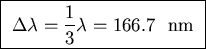 .
Note that you could get the same answer by just plugging into the
formula for the resolving power of a grating at the
.
Note that you could get the same answer by just plugging into the
formula for the resolving power of a grating at the
 principal maximum, but that wouldn't be nearly as much fun!
principal maximum, but that wouldn't be nearly as much fun!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![\fbox{ ${\displaystyle C = {2 A \over \left[ {1 \over \epsilon_1}
+ {1 \over \epsilon_2} \right] d } }$\space }](img15.gif) .
.
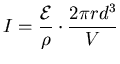 and so
and so
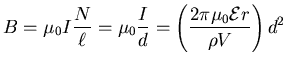 implying that short and thick is lots better,
until you start to have
implying that short and thick is lots better,
until you start to have 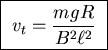 .
.

