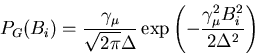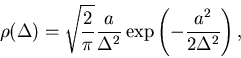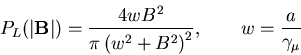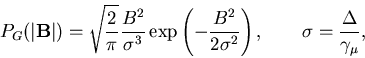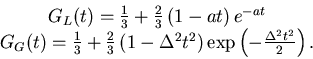

Next: Between Gaussian and Lorentzian
Up: Uemura's Site-Distribution Trick
Previous: Uemura's Site-Distribution Trick
In publications on dilute spin glass moment dynamics probed by µSR,
Uemura[1] modeled the Lorentzian field distribution at the muon site
due to the dilute spins
as a Gaussian distribution of fields at each "class'' of muon site
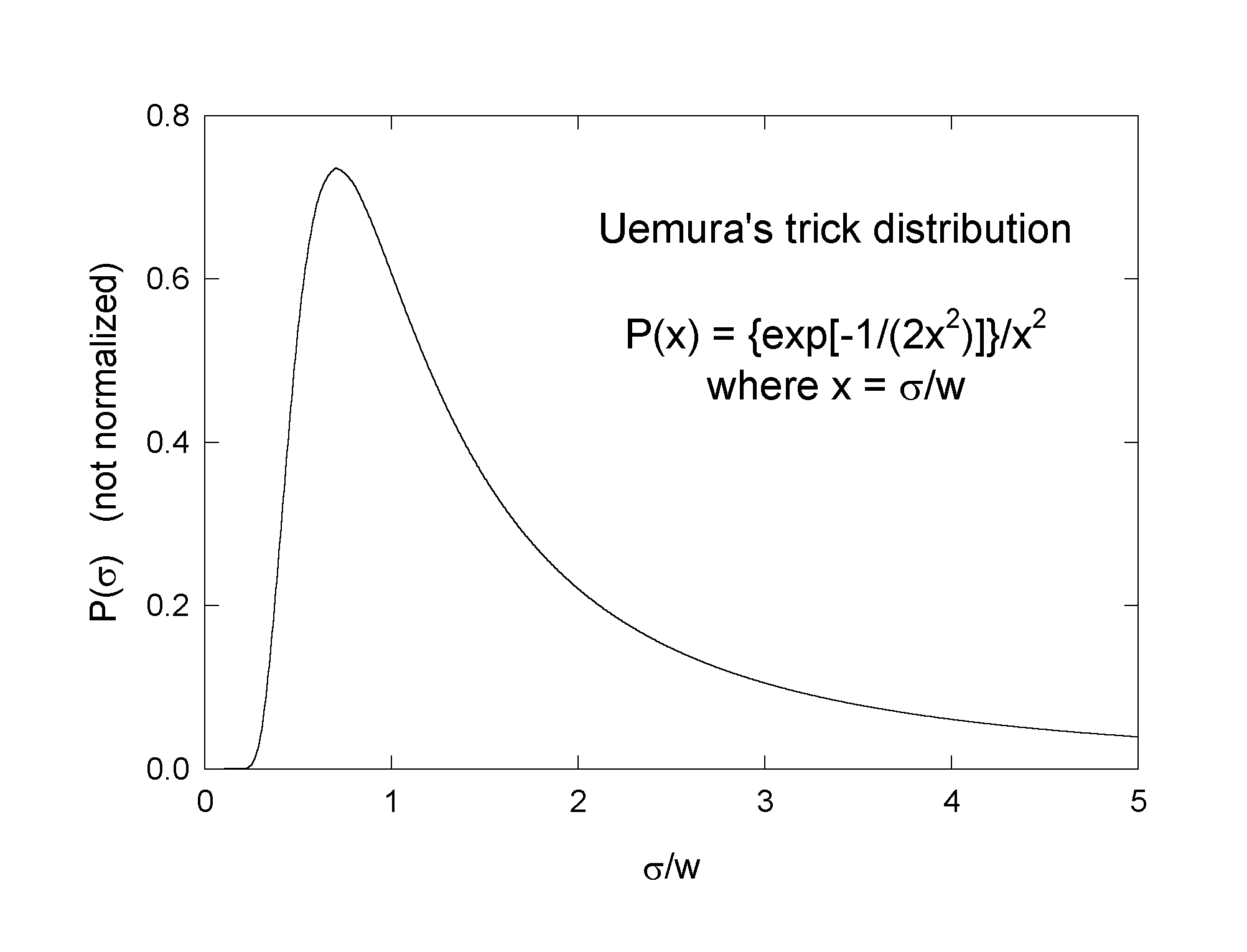
convoluted with a strange distribution of such classes of site (see Fig.1)
This convolution also works to generate the distribution of magnitudes of
field:
where
and to generate the static ZF Lorentzian Kubo-Toyabe relaxation function:
where
Figure 1: Uemura's trick distribution
In spite of the apparent strangeness
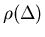 ,
Uemura was able to
use this to model moment dynamics (for a stationary muon) to produce dynamic
muon spin relaxation functions G(t) that decoupled properly in the fast
fluctuation limit (direct "dynamicization'' of the Lorentzian field
distribution, equivalent muon diffusion in a the spin glass, does not result
in fluctuation decoupling), and were consistent with observed µSR. So,
this convolution does seem to bear some relation to reality.
,
Uemura was able to
use this to model moment dynamics (for a stationary muon) to produce dynamic
muon spin relaxation functions G(t) that decoupled properly in the fast
fluctuation limit (direct "dynamicization'' of the Lorentzian field
distribution, equivalent muon diffusion in a the spin glass, does not result
in fluctuation decoupling), and were consistent with observed µSR. So,
this convolution does seem to bear some relation to reality.


Next: Between Gaussian and Lorentzian
Up: Uemura's Site-Distribution Trick
Previous: Uemura's Site-Distribution Trick
Jess H. Brewer
2002-09-24