|
Recall this picture from above. Now consider what happens
when the paramagnetic spin density fluctuates more slowly
and causes the 55Mn nuclear moments to fluctuate
(relax) faster, while at the same time beginning to have a
direct effect on the muon spins. . . .
|

|
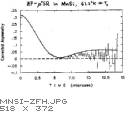
The unmistakeable characteristic signature of ``double relaxation''
of this type is when the muon polarization function falls below
the (high temperature) static gaussian ZF Gzz(t)
at early times but rises above same at late times.
This clearly cannot be due to a simple multiplication of
Gzz(t) by an additional exponential
relaxation function representing the direct effect of the
paramagnetic moments.
|

|
Excellent fits are possible over the entire temperature range
in ZF, using a constant value for the static dipolar width
(due to Mn nuclear moments) and allowing the 55Mn
and µ+ relaxation rates to vary
independently.
|



