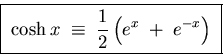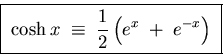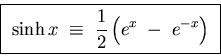Another question arises if we are familiar with the
HYPERBOLIC FUNCTIONS
These are so similar to the definitions of the 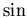 and
and 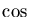 in terms of complex exponentials that we suspect a connection
between
in terms of complex exponentials that we suspect a connection
between 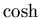 and
and 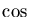 that is deeper than just the fact
that the names are so similar (which should of course have
made us suspicious in the first place). I will leave it as
a (trivial) exercise for the reader to show that
that is deeper than just the fact
that the names are so similar (which should of course have
made us suspicious in the first place). I will leave it as
a (trivial) exercise for the reader to show that


.
Jess H. Brewer -
Last modified: Sun Nov 15 14:00:22 PST 2015