 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE Wait a minute! How did I calculate h0? I had to know m for the different molecules, and that requires some knowledge of the sizes of atoms - information that has not yet been set forth in this book! In fact, empirical observations about how fast the pressure of the atmosphere does drop off with altitude could give a pretty good idea of his big atoms are; this isn't how it was done historically, but let's give it a try anyway:
Suppose that, by climbing mountains and measuring the
density of oxygen molecules (O2) as a function of altitude,
we have determined empirically that h0
for O2 is about 8,000 m.
Then, according to this simple model, it must be true
that the mass m of an O2 molecule is about
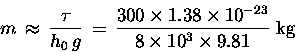
Now to mix in just a pinch of actual history: Long ago, chemists discovered (again empirically) that different pure substances combined with other pure substances in fixed ratios of small integers times a certain characteristic mass (characteristic for each pure substance) called its molecular weight A. People had a pretty good idea even then that these pure substances were made up of large numbers of identical units called "atoms,"15.24 but no one had the faintest idea how big atoms were -- except of course that they must be pretty small, since we never could see any directly. The number N0 of molecules in one molecular weight of a pure substance was (correctly) presumed to be the same, to explain why chemical reactions obeyed this rule. This number came to be called a "mole" of the substance. For oxygen (O2), the molecular weight is roughly 32 grams or 0.032 kg.
If we now combine this conventional definition of a mole
of O2 with our previous estimate of the mass of one O2
molecule, we can estimate
| (15.17) |
Turning the argument around,
the mass of a molecule can be obtained from its molecular
weight A as follows: One mole of any substance is
defined as a mass
![]() gram, and contains N0
molecules (or atoms, in the case of monatomic molecules)
of the substance.
Thus helium, with A = 4,
weighs 4 gm (or 0.004 kg) per mole containing N0 atoms,
so one He atom weighs
(0.004/N0) kg or
gram, and contains N0
molecules (or atoms, in the case of monatomic molecules)
of the substance.
Thus helium, with A = 4,
weighs 4 gm (or 0.004 kg) per mole containing N0 atoms,
so one He atom weighs
(0.004/N0) kg or
![]() kg.
kg.