Next: Back to Bohr
Up: SPIN
Previous: SPIN
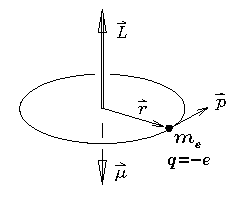 A particle of mass m in a circular orbit of radius r
has an angular momentum
A particle of mass m in a circular orbit of radius r
has an angular momentum 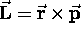 ,
where
,
where 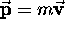 (in the nonrelativistic limit)
is the particle's momentum. Although
(in the nonrelativistic limit)
is the particle's momentum. Although 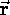 and
and 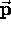 are constantly changing direction,
are constantly changing direction,  is a constant
in the absence of any torques on the system.
If the particle happens to carry an electric charge
as well as a mass (the case shown being an electron
with mass
is a constant
in the absence of any torques on the system.
If the particle happens to carry an electric charge
as well as a mass (the case shown being an electron
with mass 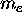 and charge -e) then the circulation of that
charge constitutes a current loop which in turn
generates a magnetic moment
and charge -e) then the circulation of that
charge constitutes a current loop which in turn
generates a magnetic moment 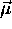 which is
inextricably "locked" to the angular momentum:
which is
inextricably "locked" to the angular momentum:
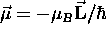 ,
where
,
where 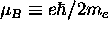 =
=
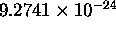 J/T
is the Bohr magneton for the case of the electron orbit.
Because the potential energy of a magnetic dipole moment
J/T
is the Bohr magneton for the case of the electron orbit.
Because the potential energy of a magnetic dipole moment
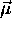 in a uniform magnetic field
in a uniform magnetic field 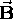 is given by
is given by 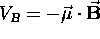 ,
the orientation of the orbit in a magnetic field
determines the contribution of its magnetic interaction
to the total energy of the state:
,
the orientation of the orbit in a magnetic field
determines the contribution of its magnetic interaction
to the total energy of the state:
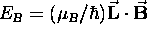 .
This contribution
is much smaller than the difference between "shells"
with different principle quantum numbers n,
and so it is called " fine structure"
in atomic spectroscopy.
.
This contribution
is much smaller than the difference between "shells"
with different principle quantum numbers n,
and so it is called " fine structure"
in atomic spectroscopy.
Jess H. Brewer -
Last modified: Mon Nov 23 13:54:00 PST 2015
 A particle of mass m in a circular orbit of radius r
has an angular momentum
A particle of mass m in a circular orbit of radius r
has an angular momentum 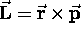 ,
where
,
where 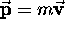 (in the nonrelativistic limit)
is the particle's momentum. Although
(in the nonrelativistic limit)
is the particle's momentum. Although 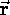 and
and 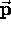 are constantly changing direction,
are constantly changing direction,  is a constant
in the absence of any torques on the system.
If the particle happens to carry an electric charge
as well as a mass (the case shown being an electron
with mass
is a constant
in the absence of any torques on the system.
If the particle happens to carry an electric charge
as well as a mass (the case shown being an electron
with mass 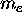 and charge -e) then the circulation of that
charge constitutes a current loop which in turn
generates a magnetic moment
and charge -e) then the circulation of that
charge constitutes a current loop which in turn
generates a magnetic moment 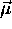 which is
inextricably "locked" to the angular momentum:
which is
inextricably "locked" to the angular momentum:
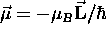 ,
where
,
where 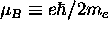 =
=
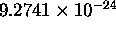 J/T
is the Bohr magneton for the case of the electron orbit.
Because the potential energy of a magnetic dipole moment
J/T
is the Bohr magneton for the case of the electron orbit.
Because the potential energy of a magnetic dipole moment
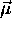 in a uniform magnetic field
in a uniform magnetic field 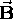 is given by
is given by 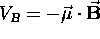 ,
the orientation of the orbit in a magnetic field
determines the contribution of its magnetic interaction
to the total energy of the state:
,
the orientation of the orbit in a magnetic field
determines the contribution of its magnetic interaction
to the total energy of the state:
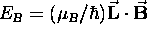 .
This contribution
is much smaller than the difference between "shells"
with different principle quantum numbers n,
and so it is called " fine structure"
in atomic spectroscopy.
.
This contribution
is much smaller than the difference between "shells"
with different principle quantum numbers n,
and so it is called " fine structure"
in atomic spectroscopy.