 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE Well, there is. It is a little tedious and complicated, but easily understood: one must make a large number of repeated measurements of the same thing and analyze the "scatter" of the answers!
Suppose we are trying to determine the "true" value of the quantity x. (We usually refer to unspecified things as "x" in this business.) It could be your pulse rate or some other simple physical observable.
We make N independent measurements
xi
![]() under as close to identical conditions as we can manage.
Each measurment, we suspect, is not terribly precise; but we
don't know just how imprecise. (It could be largely due to
some factor beyond our control; pulse rates, for instance,
fluctuate for many reasons.)
under as close to identical conditions as we can manage.
Each measurment, we suspect, is not terribly precise; but we
don't know just how imprecise. (It could be largely due to
some factor beyond our control; pulse rates, for instance,
fluctuate for many reasons.)
Now, the xi will "scatter" around the "true" x in a
distribution that will put some xi smaller than the
true x and others larger.
We assume that whatever the cause of the scatter,
it is basically random - i.e. the exact value
of one measurement xi+1 is not directly influenced by
the value xi obtained on the previous measurement.
(Actually, perfect randomness is not only hard to define,
but rather difficult to arrange in practice; it is
sufficient that most fluctuations are random enough
to justify the treatment being described here.)
It is intuitively obvious
(and can even be rigorously proved in most cases)
that our best estimate for the "true" x is the
average or mean value, ![]() ,
given
by:5.4
,
given
by:5.4
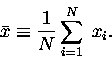 |
(5.7) |
How can we find
![]() mathematically
from the data?
Well, if we assume that each individual measurement xi
has the same single-measurement uncertainty
mathematically
from the data?
Well, if we assume that each individual measurement xi
has the same single-measurement uncertainty ![]() ,
then the distribution of xi should look like
a "bell-shaped curve"
or gaussian distribution:
,
then the distribution of xi should look like
a "bell-shaped curve"
or gaussian distribution:
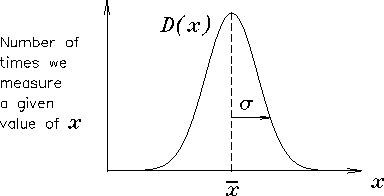 |
Obviously,
![]() is a measure of the "error"
in the
is a measure of the "error"
in the
![]() measurement,
but we cannot just find the average of
measurement,
but we cannot just find the average of
![]() ,
since by definition the sum of all
,
since by definition the sum of all
![]() is zero
(there are just as many negative errors as positive errors).
The way out of this dilemma is always to take the average of
the squares of
is zero
(there are just as many negative errors as positive errors).
The way out of this dilemma is always to take the average of
the squares of
![]() ,
which are all positive.
This "mean square" error is called
the variance, sx2:
,
which are all positive.
This "mean square" error is called
the variance, sx2:
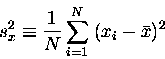 |
(5.8) |
So we actually have a way of "calculating" our
uncertainty directly from the data!
This is quite remarkable. But wait. We have not just
measured x once; we have measured it N times. Our
instincts (?) insist that our final best estimate
of x, namely the mean, ![]() ,
is determined more precisely
than we would get from just a single measurement.
This is indeed the case. The uncertainty in the mean,
,
is determined more precisely
than we would get from just a single measurement.
This is indeed the case. The uncertainty in the mean,
![]() ,
is smaller than
,
is smaller than ![]() .
By how much? Well, it takes
a bit of math to derive the answer, but you will
probably not find it implausible to accept the result
that
.
By how much? Well, it takes
a bit of math to derive the answer, but you will
probably not find it implausible to accept the result
that
![]() is smaller than
is smaller than
![]() by a factor of 1/N. That is,
by a factor of 1/N. That is,
| (5.9) |
COMMENT:The above analysis of statistical uncertainties explains how to find the best estimate (the mean) from a number N of independent measurements with unknown but similar individual uncertainties. Sometimes we can estimate the uncertainty
in each measurement xi by some independent means like "common sense" (watch out for that one!). If this is the case, and if the measurements are not all equally precise (as, for instance, in combining all the world's best measurements of some esoteric parameter in elementary particle physics), then it is wrong to give each measurement equal weight in the average. There is then a better way to define the average, namely the "weighted mean":
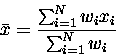
where. If the reader is interested in the proper way to estimate the uncertainty
in the mean under these circumstances, it is time to consult a statistics text; the answer is not difficult, but it needs some explanation that is beyond the scope of this HyperReference.