BELIEVE   ME   NOT!    - -     A   SKEPTIC's   GUIDE  

Algebra 2

"I'm thinking of a number, and its name is `x' ..." So if

a x² + b x + c = 0, (4.14)

what is x? Well, we can only say, "It depends." Namely, it depends on the values of a, b and c, whatever they are. Let's suppose the dimensions of all these "parameters" are mutually consistent^4.7 so that the equation makes sense. Then "it can be shown" (a classic phrase if there ever was one!) that the "answer" is generally^4.8

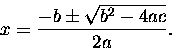$$x = {-b \pm \sqrt{b^2 - 4ac} \over 2a} .$$ (4.15)

This formula (and the preceding equation that defines what we mean by a, b and c) is known as the Quadratic Theorem, so called because it offers "the answer" to any quadratic equation (i.e. one containing powers of x up to and including x²). The power of such a general solution is prodigious. (Work out a few examples!) It also introduces an interesting new way of looking at the relationship between x and the parameters a, b and c that determine its value(s). Having x all by itself on one side of the equation and no x's anywhere on the other side is what we call a "solution" in Algebra. Let's make a simpler version of this sort of equation:

"I'm thinking of a number, and its name is `y' ..." So if y = x², what is y? The answer is again, "It depends!" (In this case, upon the value of x.) And that leads us into a new subject....