Next: The Go-Betweens
Up: High Energy Physics
Previous:
Feynman Diagrams
When quantum mechanics was first developed, it was
formulated in a nonrelativistic limit -
the particles involved were presumed not to have enough
kinetic energy to create other particles.
Because, if they did, then not only the quantum states
of each particle, but the number of particles present,
would have to be described by the theory. You can see
that the combination of quantum mechanics with relativity
makes relativistic quantum mechanics a rather more
complicated sort of problem.
Quantum mechanical equations were found for bosons
(the Klein-Gordon equation) and for fermions
(the Dirac equation)
which obeyed the correct relativistic transformations,
but now the wave functions [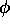 for bosons,
for bosons,
 for fermions] could not be interpreted as simply as
before - in terms of the probability amplitude for a
single particle. Now they had to be interpreted
as the probability amplitude of the field of the
corresponding particle, for which the number of
such particles was merely a quantum number of the
field.
for fermions] could not be interpreted as simply as
before - in terms of the probability amplitude for a
single particle. Now they had to be interpreted
as the probability amplitude of the field of the
corresponding particle, for which the number of
such particles was merely a quantum number of the
field.
As a result, when a particle physicist speaks of
"the electron," (s)he is referring to the electron field,
an absolutely literal example of the Platonic Ideal,
in which the disposition (and even the number) of actual
individual electrons is merely a state of the electron
[field]. An actual single individual particle in the laboratory
is rarely the source of much information about the complete
set of all its identical siblings.
A given Feynman diagram therefore represents one possible
case of the numbers and types of particles present in an
interaction with a specified initial and final state.
It is one possible manifestation of the fields.
Jess H. Brewer -
Last modified: Mon Nov 23 14:41:44 PST 2015
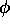 for bosons,
for bosons,
 for fermions] could not be interpreted as simply as
before - in terms of the probability amplitude for a
single particle. Now they had to be interpreted
as the probability amplitude of the field of the
corresponding particle, for which the number of
such particles was merely a quantum number of the
field.
for fermions] could not be interpreted as simply as
before - in terms of the probability amplitude for a
single particle. Now they had to be interpreted
as the probability amplitude of the field of the
corresponding particle, for which the number of
such particles was merely a quantum number of the
field.