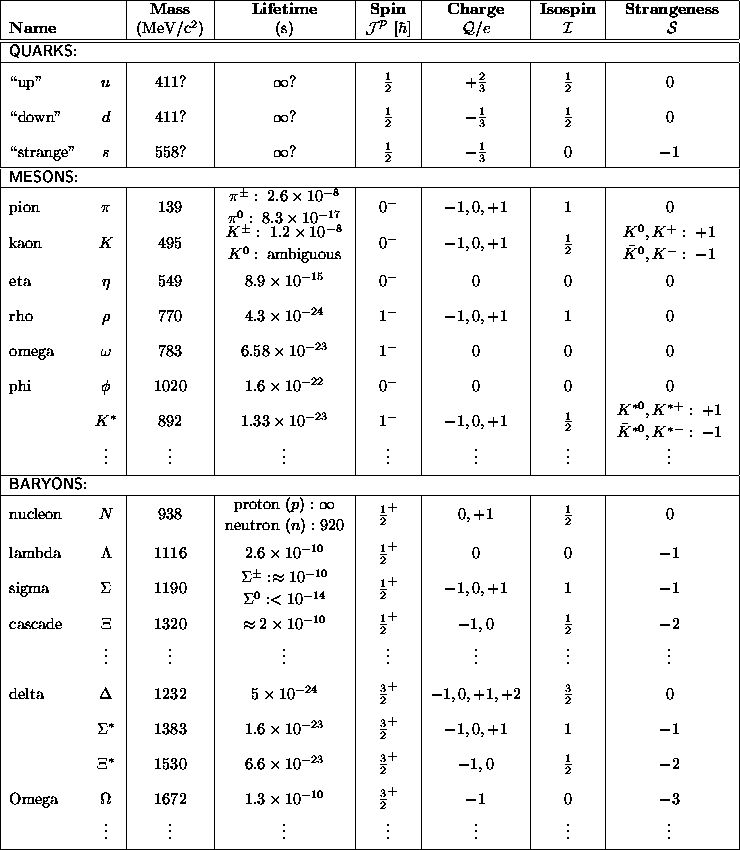
Table: Some of the hadrons (strongly interacting particles).
The remaining strongly-interacting hadrons make a huge "zoo" of mostly short-lived particles. However, these too can be separated cleanly into two dichotomous categories: the half-integer spin baryons (so named because they tend to be more heavy), which are all fermions - each type obeys its own version of the Pauli exclusion principle - and the zero or integer spin mesons (so named because they tend to me medium heavy), which are all bosons - you can put as many as you like in the same state at the same time. We now know lots of interesting things about the baryons and mesons, but the modern definitions of these classes of hadrons are in terms of their spins.

Table: Some of the hadrons (strongly interacting particles).
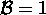 ; mesons have none.
The "hypercharge"
; mesons have none.
The "hypercharge" 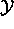 of a particle is the sum of
its baryon number and its strangeness:
of a particle is the sum of
its baryon number and its strangeness: 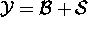 .
Quarks all have
.
Quarks all have 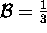 as well as fractional electric charge
because it takes 3 to make one baryon;
otherwise they follow the same rules.
For each particle (including quarks) there corresponds
an antiparticle of the same mass, spin, parity and isospin,
but with opposite values of electric charge, strangeness,
baryon number and hypercharge.
as well as fractional electric charge
because it takes 3 to make one baryon;
otherwise they follow the same rules.
For each particle (including quarks) there corresponds
an antiparticle of the same mass, spin, parity and isospin,
but with opposite values of electric charge, strangeness,
baryon number and hypercharge.
Generally speaking, all the heavy hadrons are very short-lived because the interaction governing their decay into lighter hadrons is, after all, strong. I have already mentioned a notable exception to this rule, namely the strange mesons, which take far longer than they should to decay into pions. In the 1950's this led to the coining of the term strangeness to describe that strange (grrr...) property of K mesons (for instance) that could not be "swept under the rug" by the strong interaction. By checking to see what other particles could decay into kaons, and in the company of what else, a strangeness was assigned to each of the hadrons. Then a strange [Oops! Can't use that!] - an odd [Ouch! That implies a parity quantum number] - a peculiar [Whew!] pattern began to manifest itself when the particles were grouped together according to the known quantifiable properties of spin, charge, strangeness and mass.
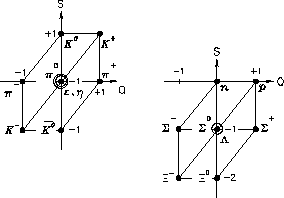
Figure:
Murray Gell-Mann's "Eightfold Way."
Left: the scalar mesons.
Right: the spin-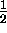 baryons.
baryons.
 is plotted against
charge Q.
The vector (spin 1) mesons form a group
exactly like the scalar mesons on the left,
further reinforcing the pattern.
is plotted against
charge Q.
The vector (spin 1) mesons form a group
exactly like the scalar mesons on the left,
further reinforcing the pattern.
The various hadrons are first separated into collections that
all have the same spin,
such as the scalar [zero spin] mesons
or the vector [spin 1] mesons
or the spin-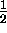 baryons
or the spin-
baryons
or the spin-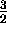 baryons.
It is immediately evident that the masses
of all the particles in any one of these groups
are roughly similar, whereas two different groups
tend to have significantly different masses.
This arouses some suspicion.
Then we notice that, within these groups, the particles
with the most strangeness tend to be the heaviest.
baryons.
It is immediately evident that the masses
of all the particles in any one of these groups
are roughly similar, whereas two different groups
tend to have significantly different masses.
This arouses some suspicion.
Then we notice that, within these groups, the particles
with the most strangeness tend to be the heaviest.
Next we notice that if we plot the particles in a group
on a graph of the two other quantifiable properties -
charge Q and strangeness 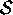 -
they form arrangements that are remarkably similar
in shape!
-
they form arrangements that are remarkably similar
in shape!![]() The hexagonal arrangement with two particles at the centre
appears in each of the first three groupings listed above;
Murray Gell-Mann decided that this must mean something
about the constituents of these particles, just as
the regular groupings of elements in the Periodic Table
meant something about the constituents of atoms.
Because of the number of particles in the pattern,
because of his eclectic intellect and because he wanted to
make up a catchy name for his theory that people would want
to talk about just to sound savvy, Murray named this pattern
the eightfold way after the spiritual/behavioural
prescription in Buddhism. More cuteness.
The hexagonal arrangement with two particles at the centre
appears in each of the first three groupings listed above;
Murray Gell-Mann decided that this must mean something
about the constituents of these particles, just as
the regular groupings of elements in the Periodic Table
meant something about the constituents of atoms.
Because of the number of particles in the pattern,
because of his eclectic intellect and because he wanted to
make up a catchy name for his theory that people would want
to talk about just to sound savvy, Murray named this pattern
the eightfold way after the spiritual/behavioural
prescription in Buddhism. More cuteness.