BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Tides
Up: Orbital Mechanics
Previous: Changing Orbits
We can now explain (at least for circular orbits) Kepler's Third Law.
The period T of an orbit is the circumference 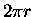 divided by the speed of travel, v. Using the equation above
for v in terms of r gives
divided by the speed of travel, v. Using the equation above
for v in terms of r gives
as observed by Kepler. Newton explained why.
Jess H. Brewer -
Last modified: Sat Nov 14 12:31:10 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE 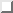 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE