BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Up: Magnetic Units
Previous: Magnetic Units
There are two "accepted" units for the magnetic field 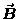 :
GAUSS [abbreviated G] and TESLA [abbreviated T].
Needless to say, both are named after great
:
GAUSS [abbreviated G] and TESLA [abbreviated T].
Needless to say, both are named after great
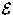 &
&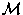 researchers.
The former is handy when describing weak magnetic fields -
for instance, the Earth's magnetic field is on the order of 1 G -
but the unit that goes best with our selected electrical units
(because it is defined in terms of meters and coulombs and seconds)
is the TESLA. Fortunately the conversion factor is simple:
researchers.
The former is handy when describing weak magnetic fields -
for instance, the Earth's magnetic field is on the order of 1 G -
but the unit that goes best with our selected electrical units
(because it is defined in terms of meters and coulombs and seconds)
is the TESLA. Fortunately the conversion factor is simple:
The TESLA is also defined in terms of the WEBER [W]
(named after guess whom), a conventional unit of magnetic flux.
The definition is
if you're interested.
So referring back to Eq. (8), we have
which we can rearrange to read
so that kM must have dimensions of
magnetic flux per unit current per unit length
or units of W/A-m.
Its value is again determined by experiment:
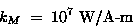 |
(17.20) |
I will leave it as an exercise for the student
to plug these coupling constants back into the equations
where they appear and show that everything is, though weird,
dimensionally consistent.


Up: Magnetic Units
Previous: Magnetic Units
Jess H. Brewer -
Last modified: Mon Nov 16 17:17:47 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE