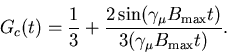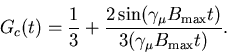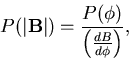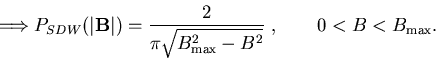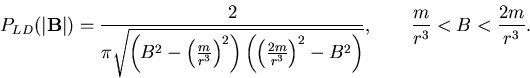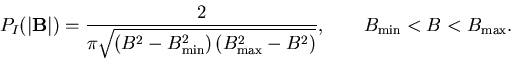

Next: Bibliography
Up: An Ornamental Garden of Field Distributions and Static
Previous: Monotonic-decreasing field-magnitude distributions
Long-range magnetic ordering incommensurate with the lattice is generally
expected to generate broad field distributions at each crystallographic muon
site in the material. In theory, this can still result in quite distinctive
muon spin relaxation functions, even though real-world observation of
µSR in incommensurate magnets has generally been disappointing.
Generally,
for an interstitial muon site in a lattice with local moments in a long
range ordered state, there should be a strict upper-limit cutoff field
magnitude, so in some sense the broadest possible field-magnitude
distribution is
 ,
for
,
for
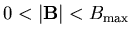 .
In
spite of the broadness, this distribution causes a static ZF µSR
relaxation function with clear oscillations. By direct integration
.
In
spite of the broadness, this distribution causes a static ZF µSR
relaxation function with clear oscillations. By direct integration
Note that the fequency seen is not representative of some average of the
fields in the distribution, but of the highest field involved in the
distribution.
For a simple amplitude-modulation spin density wave (SDW) magnetic ordering,
if the local field is assumed to be proportional to the local amplitude of
the SDW,
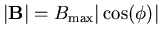 ,
with all values of
,
with all values of 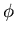 equally likely.
equally likely.
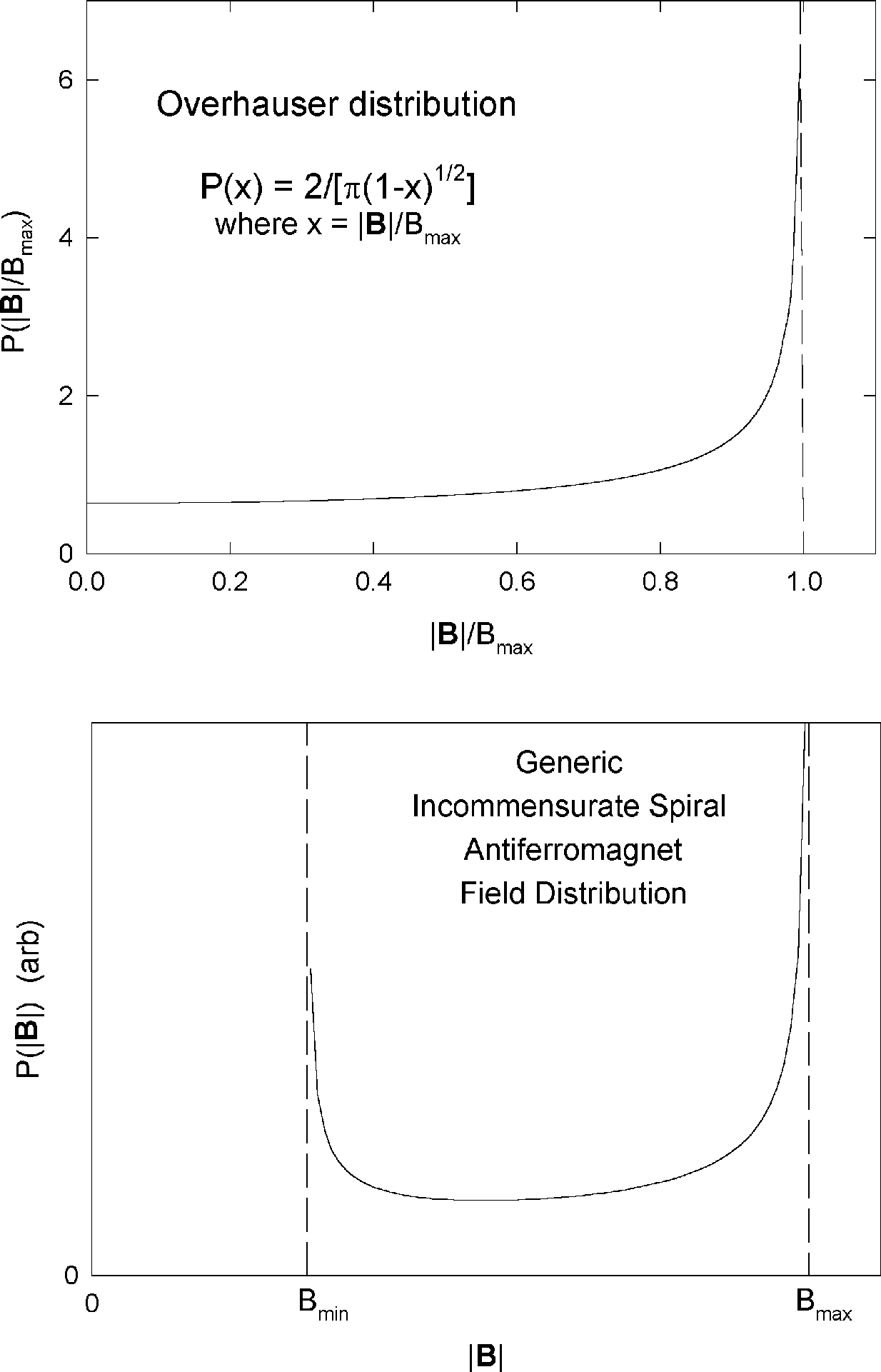
Peretto et al.,[5] considering perturbed angular correlation
(PAC) in chromium metal, call this the "Overhauser" distribution, and
discuss PAC relaxation functions (slightly different than for µSR) in
terms of J0, the zero-order Bessel function. The static ZF µSR
function is
After some initial relaxation, this also settles down to oscillation at the
maximum field frequency of the distribution.
To model µSR in a helical incommensurate magnetic ordered state,
consider a single host moment to be closest to the muon site, and let the
orientation of that moment point anywhere in a plane containing both the
host moment and the muon positions, for fixed muon polarization direction.
If there is only dipole coupling between host moment and muon spin,
where, in a simple case, m and 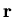 are fixed, and all values of
are fixed, and all values of 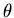 are equally probable. In this case
are equally probable. In this case 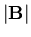 ranges between
ranges between
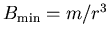 and
and
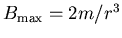 .
If the plane of host moment
orientation does not contain the muon,
.
If the plane of host moment
orientation does not contain the muon, 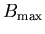 is reduced. In the
simplest "lone dipole" case, then,
is reduced. In the
simplest "lone dipole" case, then,
This distribution diverges as B goes to either 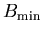 or
or 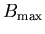 .
Numerical simulations[6] indicate that for muons dipole coupled to
all the host moments in an incommensurate ordering in which the moments
point anywhere in a plane the local field distribution has this form except
that
.
Numerical simulations[6] indicate that for muons dipole coupled to
all the host moments in an incommensurate ordering in which the moments
point anywhere in a plane the local field distribution has this form except
that 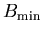 and
and 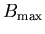 are essentially independent parameters, and
in particular,
are essentially independent parameters, and
in particular, 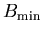 can also be less than
can also be less than
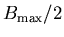 .
This
suggests that a generic incommensurate antiferromagnet muon-site field
distribution might be
.
This
suggests that a generic incommensurate antiferromagnet muon-site field
distribution might be
Note that
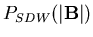 is the
is the
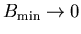 limit of
limit of
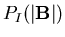 .
This distribution is likely to generate a static ZF
relaxation function with 2 frequencies, corresponding to the upper and lower
limits of the distribution.
.
This distribution is likely to generate a static ZF
relaxation function with 2 frequencies, corresponding to the upper and lower
limits of the distribution.
Figure 6:

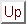

Next: Bibliography
Up: An Ornamental Garden of Field Distributions and Static
Previous: Monotonic-decreasing field-magnitude distributions
Jess H. Brewer
2002-09-24